题目内容
8．椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的焦点为F1，F2，P为椭圆上一点，若|PF1|=2，则|PF2|=6．分析 利用椭圆得定义|PF1|+|PF2|=2a列式求解即可．
解答 解：因为P为椭圆上一点，F1，F2，为椭圆的焦点，所以|PF1|+|PF2|=2a=8，
又|PF1|=2，则|PF2|=8-|PF1|=6．
所以答案应为：6
点评 本题主要考查了椭圆定义的应用，属于简单题型．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
10．命题“对任意的x∈R，x2≥0”的否定是（ ）
| A． | 对任意的x∈R，x2＜0 | B． | 不存在x∈R，x2＜0 | ||
| C． | 存在x∈R，x2＜0 | D． | 存在x∈R，x2≥0 |
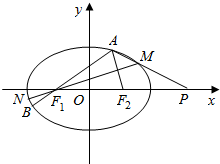已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$．A为椭圆C上一动点（A异于左、右顶点），F1、F2分别为椭圆C的左、右焦点，且△AF1F2面积的最大值为1；