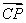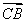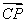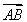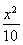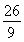Question

知数列{an}是首项为，公比为的等比数列，设bn＋15log3an＝t，常数t∈N*.

(1)求证：{bn}为等差数列；

(2)设数列{cn}满足cn＝anbn，是否存在正整数k，使ck，ck＋1，ck＋2按某种次序排列后成等比数列？若存在，求k，t的值；若不存在，请说明理由．

 

Answer 1

（1）见解析（2）存在k＝1，t＝5

【解析】(1) an＝3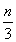－，bn＋1－bn＝－15log3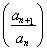＝5，

∴{bn}是首项为b1＝t＋5，公差为5的等差数列．

(2)cn＝(5n＋t) ·3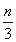－，则ck＝(5k＋t)·3－，

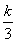令5k＋t＝x(x>0)，则ck＝x·3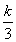－，ck＋1＝(x＋5)·3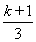－，ck＋2＝(x＋10)·3－.

①若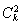＝ck＋1ck＋2，则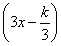2＝(x＋5)·3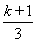－·(x＋10)·3－.

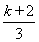化简得2x2－15x－50＝0，解得x＝10；进而求得k＝1，t＝5；

②若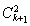＝ckck＋2，同理可得(x＋5)2＝x(x＋10)，显然无解；

③若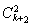＝ckck＋1，同理可得 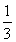(x＋10)2＝x(x＋5)，方程无整数根．

综上所述，存在k＝1，t＝5适合题意．