题目内容

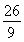已知圆心角为120°的扇形AOB的半径为1，C为的中点，点D，E分别在半径OA，OB上．若CD2＋CE2＋DE2＝，则OD＋OE的最大值是________．

 

【解析】在△COD中，由余弦定理得CD2＝1＋OD2－OD，同理在△EOC、△DOE中，由余弦定理分别得CE2＝1＋OE2－OE，DE2＝OE2＋OD2＋OD·OE，代入CD2＋CE2＋DE2＝整理得2(OD＋OE)2－(OE＋OD)－＝3OD·OE，由基本不等式得3OD·OE≤，

所以2(OD＋OE)2－(OE＋OD)－≤，解得0≤OD＋OE≤，即OD＋OE的最大值是.

 

练习册系列答案
相关题目

知数列{an}是首项为，公比为的等比数列，设bn＋15log3an＝t，常数t∈N*.

(1)求证：{bn}为等差数列；

(2)设数列{cn}满足cn＝anbn，是否存在正整数k，使ck，ck＋1，ck＋2按某种次序排列后成等比数列？若存在，求k，t的值；若不存在，请说明理由．

 

已知函数f(x)＝Acos(ωx＋φ)(A>0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝”的______条件．

 

已知函数f(x)＝aln x＋x在区间[2,3]上单调递增，则实数a的取值范围是________．

 

已知函数f(x)＝x2＋bx＋c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)．

(1)证明：当x≥0时，f(x)≤(x＋c)2；

(2)若对满足题设条件的任意b，c，不等式f(c)－f(b)≤M(c2－b2)恒成立，求M的最小值．

 

已知a>0，b>0，且2a＋b＝4，则的最小值为________．

 

一块形状为直角三角形的铁皮，两直角边长分别为40 cm、60 cm，现要将它剪成一个矩形，并以此三角形的直角为矩形的一个角，则矩形的最大面积是________cm2.

 

袋中装有大小相同且形状一样的四个球，四个球上分别标有“2”、“3”、“4”、“6”这四个数．现从中随机选取三个球，则所选的三个球上的数恰好能构成一个等差数列的概率是________．

 

求证：1＋2＋22＋…＋25n－1能被31整除．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网