题目内容
14.已知函数y=cosx的定义域为[a,b].值域为[-1,$\frac{\sqrt{2}}{2}$],则b-a的值不可能是( )| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{5π}{4}$ |
分析 由题意和余弦函数的图象可知b-a的值应不小于$\frac{3π}{4}$,结合选项可得.
解答 解:∵函数y=cosx的定义域为[a,b].值域为[-1,$\frac{\sqrt{2}}{2}$],
∴结合余弦函数图象可知y取-1和$\frac{\sqrt{2}}{2}$的最近的x值相差π-$\frac{π}{4}$=$\frac{3π}{4}$,
故b-a的值应不小于$\frac{3π}{4}$
故选:A
点评 本题考查余弦函数的定义域和值域,属基础题.

练习册系列答案
相关题目
 已知f(x)=$\left\{\begin{array}{l}{-x,-1≤x<0}\\{{x}^{2},0≤x<1}\\{x,1≤x≤2}\end{array}\right.$
已知f(x)=$\left\{\begin{array}{l}{-x,-1≤x<0}\\{{x}^{2},0≤x<1}\\{x,1≤x≤2}\end{array}\right.$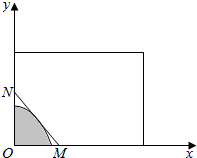 如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M,N.则△MON面积的最小值为$\frac{2}{3}$.
如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M,N.则△MON面积的最小值为$\frac{2}{3}$.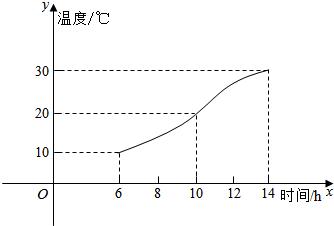 如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.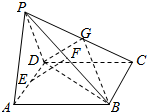 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.设AD、PB、PC中点分别为E、F、G.
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.设AD、PB、PC中点分别为E、F、G.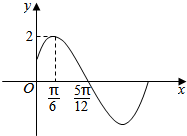 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.