题目内容
2.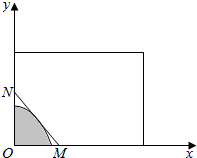 如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M,N.则△MON面积的最小值为$\frac{2}{3}$.
如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M,N.则△MON面积的最小值为$\frac{2}{3}$.
分析 设MN为曲线y=1-$\frac{4}{3}$x2的切线,切点为(m,n),由抛物线的方程,求出导数,求得切线的斜率,运用点斜式方程可得切线的方程,分别令x=0,y=0可得M,N的坐标,求得△MNO的面积,再由导数求得单调区间和极小值,也为最小值,即可得到所求值.
解答 解:设MN为曲线y=1-$\frac{4}{3}$x2的切线,切点为(m,n),
可得n=1-$\frac{4}{3}$m2,y=1-$\frac{4}{3}$x2的导数为y′=-$\frac{8}{3}$x,
即有直线MN的方程为y-(1-$\frac{4}{3}$m2)=-$\frac{8}{3}$m(x-m),
令x=0,可得y=1+$\frac{4}{3}$m2,再令y=0,可得x=$\frac{3+4{m}^{2}}{8m}$(m>0),
即有△MON面积为S=$\frac{1}{2}$(1+$\frac{4}{3}$m2)•$\frac{3+4{m}^{2}}{8m}$=$\frac{9+16{m}^{4}+24{m}^{2}}{48m}$,
由S′=$\frac{1}{48}$(-$\frac{9}{{m}^{2}}$+48m2+24)=0,解得m=$\frac{1}{2}$,
当m>$\frac{1}{2}$时,S′>0,函数S递增;当0<m<$\frac{1}{2}$时,S′<0,函数S递减.
即有m=$\frac{1}{2}$处取得最小值,且为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查三角形的面积的最值的求法,注意运用函数的导数,求得切线方程,再由单调性求最值,考查运算能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
14.已知函数y=cosx的定义域为[a,b].值域为[-1,$\frac{\sqrt{2}}{2}$],则b-a的值不可能是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{5π}{4}$ |