题目内容
9.已知直线l1:x+my+9=0和直线l2:(m-2)x+3y+3m=0,m为何值时,直线l1与l2为(1)重合;
(2)平行;
(3)垂直.
分析 解方程1×3-m(m-2)=0可得平行或重合;解m-2+3m=0可得垂直.
解答 解:由1×3-m(m-2)=0可解得m=-1或m=3,
当m=-1时,直线l1:x-y+9=0,
直线l2:-3x+3y-3=0,即x-y+1=0,两直线平行;
当m=3时,直线l1:x+3y+9=0,
直线l2:x+3y+9=0,两直线重合;
故(1)m=3时,两直线重合;
(2)当m=-1时,两直线平行;
(3)由m-2+3m=0可解得m=$\frac{1}{2}$,
此时两直线垂直.
点评 本题考查直线的一般式方程和平行垂直关系,属基础题.

练习册系列答案
相关题目
20. 一个直三棱柱的三视图如图所示,其中俯视图是一个顶角为120°的等腰三角形,则该直三棱柱外接球的表面积为( )
一个直三棱柱的三视图如图所示,其中俯视图是一个顶角为120°的等腰三角形,则该直三棱柱外接球的表面积为( )
 一个直三棱柱的三视图如图所示,其中俯视图是一个顶角为120°的等腰三角形,则该直三棱柱外接球的表面积为( )
一个直三棱柱的三视图如图所示,其中俯视图是一个顶角为120°的等腰三角形,则该直三棱柱外接球的表面积为( )| A. | 20π | B. | $\frac{20\sqrt{5}}{3}$π | C. | 25π | D. | 25$\sqrt{5}$π |
14.已知函数y=cosx的定义域为[a,b].值域为[-1,$\frac{\sqrt{2}}{2}$],则b-a的值不可能是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{5π}{4}$ |
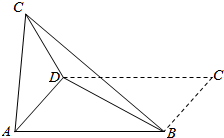 在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:
在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求: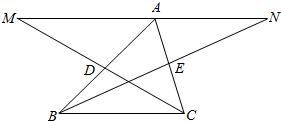 如图所示,已知D,E分别为△ABC的边AB,AC的中点,延长CD到M使DM=CD,延长BE至N使BE=EN.求证:M,A,N三点共线.
如图所示,已知D,E分别为△ABC的边AB,AC的中点,延长CD到M使DM=CD,延长BE至N使BE=EN.求证:M,A,N三点共线.