题目内容
3.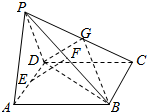 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.设AD、PB、PC中点分别为E、F、G.
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.设AD、PB、PC中点分别为E、F、G.(Ⅰ)求证:PB⊥AD;
(Ⅱ)求证:EF∥平面PCD;
(Ⅲ)若PB=$\sqrt{6}$,求四面体G-BCD的体积.
分析 (Ⅰ)连结PE、BE,由已知得PE⊥AD,BE⊥AD,从而AD⊥平面BPE,由此能证明PB⊥AD.
(Ⅱ)连结AC,交BD于O,连结EO、FO,由已知得OE∥CD,OF∥PD,从而平面EFO∥平面PDC,由此能证明EF∥平面PCD.
(Ⅲ)由PB=$\sqrt{6}$,由勾股定理得PE=$\sqrt{3}$,G到平面BDC的距离为$\frac{1}{2}PE=\frac{\sqrt{3}}{2}$,由此能求出四面体G-BCD的体积.
解答 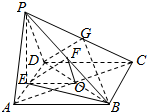 证明:(Ⅰ)连结PE、BE,
证明:(Ⅰ)连结PE、BE,
∵底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°,AD、PB、PC中点分别为E、F、G,
∴PE⊥AD,BE⊥AD,
∵PE∩BE=E,∴AD⊥平面BPE,
∵PB?平面BPE,∴PB⊥AD.
(Ⅱ)连结AC,交BD于O,连结EO、FO,
∵AD、PB中点分别为E、F,∴OE∥CD,OF∥PD,
∵EO∩FO=O,PD∩DC=D,
∴平面EFO∥平面PDC,
∵EF?平面EFO,∴EF∥平面PCD.
解:(Ⅲ)∵PB=$\sqrt{6}$,BE=$\sqrt{4-1}$=$\sqrt{3}$,∴PE=$\sqrt{6-3}$=$\sqrt{3}$,
${S}_{△BDC}=\frac{1}{2}×BC×BE$=$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$,
∵G是PC的中点,∴G到平面BDC的距离为$\frac{1}{2}PE=\frac{\sqrt{3}}{2}$,
∴四面体G-BCD的体积V=$\frac{1}{3}×{S}_{△BDC}×(\frac{1}{2}PE)$=$\frac{1}{3}×\sqrt{3}×\frac{\sqrt{3}}{2}$=$\frac{1}{2}$.
点评 本题考查异面直线垂直的证明,考查线面平行的证明,生查四面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{5π}{4}$ |
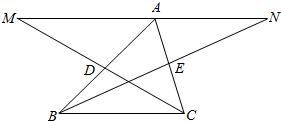 如图所示,已知D,E分别为△ABC的边AB,AC的中点,延长CD到M使DM=CD,延长BE至N使BE=EN.求证:M,A,N三点共线.
如图所示,已知D,E分别为△ABC的边AB,AC的中点,延长CD到M使DM=CD,延长BE至N使BE=EN.求证:M,A,N三点共线.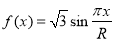 的图象上,相邻的一个最大值点与一个最小值点恰好在圆
的图象上,相邻的一个最大值点与一个最小值点恰好在圆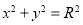 上,则
上,则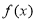 的最小正周期为( )
的最小正周期为( )