题目内容
4.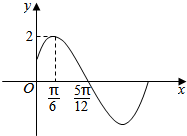 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.(1)求函数y=f(x)的解析式;
(2)求函数在x∈[-π,π]上的单调减区间;
(3)将函数y=f(x)的图象向右平移$\frac{π}{4}$个单位,得到y=g(x)的图象,若方程g(x)=m在(0,π)内有两个不同的实数根,求实数m的取值范围以及这两个根的和.
分析 (1)由图象观察可得A,T,故可求ω=2,由点($\frac{5π}{12}$,0)在图象上,可求φ,从而可求函数的解析式;
(2)由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z可解得函数在x∈[-π,π]上的单调减区间;
(3)设x∈(-$\frac{π}{4}$,$\frac{3π}{4}$),且方程f(x)=m有两个不同的实数根,通过函数的图象结合函数的对称轴,直接求实数m的取值范围和这两个根的和.
解答 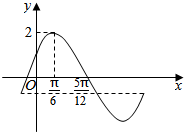 解:(1)由图象观察可知:A=2,T=4($\frac{5π}{12}$-$\frac{π}{6}$)=π,故ω=2,
解:(1)由图象观察可知:A=2,T=4($\frac{5π}{12}$-$\frac{π}{6}$)=π,故ω=2,
∵点($\frac{5π}{12}$,0)在图象上,
∴2sin(2×$\frac{5π}{12}$+φ)=0,
∴$\frac{5π}{6}$+φ=kπ,k∈Z,
∴可解得:φ=kπ-$\frac{5π}{6}$,k∈Z,
∵|φ|<π
∴φ=$\frac{π}{6}$.
∴f(x)=2sin(2x+$\frac{π}{6}$).
(2)由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z可解得:x∈[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z
故在x∈[-π,π]上的单调减区间为:[-$\frac{5π}{6}$,-$\frac{π}{3}$],[$\frac{π}{6}$,$\frac{2π}{3}$].
(3)将函数y=f(x)的图象向右平移$\frac{π}{4}$个单位,得到y=g(x)=2sin(2x-$\frac{π}{3}$)
如图所示,在同一坐标系中画出y=2sin(2x+$\frac{π}{6}$)和y=m(x∈(-$\frac{π}{4}$,$\frac{3π}{4}$)的图象,
由图可知,当-2<m<-$\frac{\sqrt{3}}{2}$或-$\frac{\sqrt{3}}{2}$<m<2时,直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根.
∴m的取值范围为:-2<m<-$\frac{\sqrt{3}}{2}$或-$\frac{\sqrt{3}}{2}$<m<2;
当-2<m<-$\frac{\sqrt{3}}{2}$时,两根和为$\frac{π}{6}$;当-$\frac{\sqrt{3}}{2}$<m<2时,两根和为$\frac{7π}{6}$.
∵方程g(x)=m在(0,π)内有两个不同的实数根,
∴当-2<m<-$\frac{\sqrt{3}}{2}$时,两根和为$\frac{5π}{12}$;当-$\frac{\sqrt{3}}{2}$<m<2时,两根和为$\frac{17π}{12}$.
点评 本题主要考查了三角函数的解析式的求法,三角函数的图象的应用,考查计算能力,是常考题型,属于中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{5π}{4}$ |
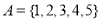 ,
,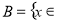 R│
R│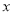 ≥
≥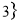 ,下图中阴影部分所表示的集合为
,下图中阴影部分所表示的集合为 
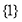 B.
B.
 D.
D.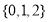
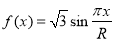 的图象上,相邻的一个最大值点与一个最小值点恰好在圆
的图象上,相邻的一个最大值点与一个最小值点恰好在圆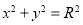 上,则
上,则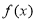 的最小正周期为( )
的最小正周期为( ) 的离心率
的离心率 ,则
,则 .
.