��Ŀ����
17�����������е��������У�����������9������һö����Ӳ�ҵ����飬�����5�γ������棬��ˣ���������ĸ�����$\frac{5}{9}$��
�ں�����װ�д�С���ȵ�3������3������2��������ôÿ����ɫ���������Ŀ�������ͬ��
�۴�-4��-3��-2��-1��0��1��2����ȡһ������ȡ�õ���С��0�Ͳ�С��0�Ŀ�������ͬ��
�ֱܷ��2��������3��Ů���и�ѡһ����Ϊ��������ôÿ��ѧ����ѡ�еĿ�������ͬ��
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
���� ��ʵ�����̫�٣���ѡ�����
��������ɫ��������ͬ����ѡ�����
��С��0�����0�����ֲ���ͬ����ѡ�����
��������Ů����ѡ�еĿ����Բ�ͬ����ѡ�����
��� �⣺��ʵ�����̫�٣���������ø���ӦΪ$\frac{1}{2}$����ѡ�����
��������ɫ��������ͬ���������������ĸ���Ϊ$\frac{3}{8}$����������ĸ���Ϊ$\frac{2}{8}$=$\frac{1}{4}$����ѡ�����
��С��0�����0�����ֲ���ͬ��ȡ����С��0�ĸ���Ϊ$\frac{4}{7}$��ȡ�����ִ���0�ĸ���Ϊ$\frac{2}{7}$����ѡ�����
��������Ů����ѡ�еĿ����Բ�ͬ������ѡ�еĸ���Ϊ$\frac{1}{2}$��Ů��ѡ�еĸ���Ϊ$\frac{1}{3}$����ѡ�����
��ѡ��A��
���� ���⿼�������������ж���Ӧ�ã�������Եĸ����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
5��ij�����������ͼ��ͼ����ü���������Ϊ��������


| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | 2 | D�� | 3 |
5��ͨ���г����飬�õ�ij��Ʒ���ʽ�Ͷ��x����Ԫ�����õ�����y����Ԫ�������ݣ����±���ʾ��
�ο���ʽ��$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$
��1���������ݶ�Ӧ��ɢ��ͼ��
��2�������ϱ��ṩ�����ݣ�����С���˷������Իع�ֱ�߷���$\widehat{y}$=bx+a��
��3����Ͷ���ʽ�10����Ԫ��������ƻ�õ�����Ϊ������Ԫ��
| �ʽ�Ͷ��x | 2 | 3 | 4 | 5 | 6 |
| ����y | 2 | 3 | 5 | 6 | 9 |
��1���������ݶ�Ӧ��ɢ��ͼ��
��2�������ϱ��ṩ�����ݣ�����С���˷������Իع�ֱ�߷���$\widehat{y}$=bx+a��
��3����Ͷ���ʽ�10����Ԫ��������ƻ�õ�����Ϊ������Ԫ��
2��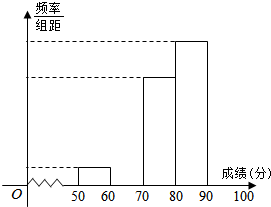 �����ꡰ��������������Խ��Խ��������ע��ijУ�Ը�һ600��ѧ��������һ�Ρ�����������֪ʶ���ԣ������г�ȡ�˲���ѧ���ijɼ����÷�ȡ������������100�֣���Ϊ������������������δ��ɵ�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��
�����ꡰ��������������Խ��Խ��������ע��ijУ�Ը�һ600��ѧ��������һ�Ρ�����������֪ʶ���ԣ������г�ȡ�˲���ѧ���ijɼ����÷�ȡ������������100�֣���Ϊ������������������δ��ɵ�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��
��1����д�����Ƶ�ʷֲ����еĿո���ȫƵ�ʷֲ�ֱ��ͼ��
��2���Թ��Ƹ���γɼ���[70��90���ε��ж����ˣ�
��3������������ε�ƽ���֣�
 �����ꡰ��������������Խ��Խ��������ע��ijУ�Ը�һ600��ѧ��������һ�Ρ�����������֪ʶ���ԣ������г�ȡ�˲���ѧ���ijɼ����÷�ȡ������������100�֣���Ϊ������������������δ��ɵ�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��
�����ꡰ��������������Խ��Խ��������ע��ijУ�Ը�һ600��ѧ��������һ�Ρ�����������֪ʶ���ԣ������г�ȡ�˲���ѧ���ijɼ����÷�ȡ������������100�֣���Ϊ������������������δ��ɵ�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ����1����д�����Ƶ�ʷֲ����еĿո���ȫƵ�ʷֲ�ֱ��ͼ��
��2���Թ��Ƹ���γɼ���[70��90���ε��ж����ˣ�
��3������������ε�ƽ���֣�
| ���� | Ƶ�� | Ƶ�� |
| [50��60�� | 2 | 0.04 |
| [60��70�� | 8 | 0.16 |
| [70��80�� | 10 | |
| [80��90�� | ||
| [90��100] | 14 | 0.28 |
| �ϼ� | 1.00 |
6������ѧ�ۺ���������ij��ά�ȵIJ����У��֡����㡢�ϸ��д��Ľ��������ȼ�����ѧ��������ijУ�߶��꼶������500�ˣ�Ů��400�ˣ�Ϊ���˽��Ա�Ը�ά�Ȳ��������Ӱ�죬���÷ֲ���������Ӹ߶��꼶��ȡ��45��ѧ���IJ��������������Ƶ��ͳ�Ʊ����£�
��1������
��2����
��1���ӱ�2�ķ�����ѧ�������ѡȡ2�˽�̸������ѡ2����ǡ��1�˲����ȼ�Ϊ�ϸ�ĸ��ʣ�
��2���ɱ���ͳ��������д�±�2��2�����������ж��Ƿ���90%�İ�����Ϊ����������������Ա��йء���
�ο������빫ʽ��K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$�ٽ�ֵ��
��1������
| �ȼ� | ���� | �ϸ� | �д��Ľ� |
| Ƶ�� | 15 | x | 5 |
| �ȼ� | ���� | �ϸ� | �д��Ľ� |
| Ƶ�� | 15 | 3 | y |
��2���ɱ���ͳ��������д�±�2��2�����������ж��Ƿ���90%�İ�����Ϊ����������������Ա��йء���
| ���� | Ů�� | �ܼ� | |
| ���� | |||
| ������ | |||
| �ܼ� |
| P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |