题目内容
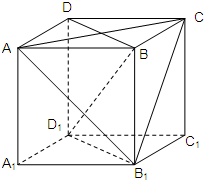
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱BC,CC1,C1D1,AA1的中点,O为AC与BD的交点.
(1)求证:平面BDF∥平面B1D1H;
(2)求证:平面BDF⊥平面A1AO;
(3)求证:EG⊥AC.
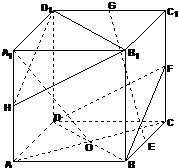
(1)求证:平面BDF∥平面B1D1H;
(2)求证:平面BDF⊥平面A1AO;
(3)求证:EG⊥AC.

证明:(1)正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱BC,CC1,C1D1,AA1的中点,∴B1D1∥BD.
∵BD?平面BDF,而B1D1不在平面BDF 内,∴B1D1∥平面BDF.
取DD1的中点N,则 AH∥D1N 且AH=D1N,故AHND1为平行四边形,∴HD1∥AN.
同理可证 BF∥AN,故HD1∥BF.
∵BF?平面BDF,而HD1不在平面BDF 内,∴HD1∥平面BDF.
这样,在平面平面B1D1H 内有两条相交直线B1D1和HD1都和平面BDF平行,
∴平面BDF∥平面B1D1H.
(2)∵O为AC与BD的交点,∴BD⊥AO.再由A1A⊥平面ABCD可得 A1A⊥BD.
故BD垂直于平面平面A1AO中的两条相交直线AO和A1A,∴BD⊥平面A1AO.
而BD?平面BDF,∴平面BDF⊥平面A1AO.
(3)取CD的中点M,连接EM,GM,则EM是△CBD的中位线,∴EM∥BD,由AC⊥BD 可得 EM⊥AC.
由GM和棱A1A平行可得GM⊥平面ABCD,GM⊥AC.
这样,AC垂直于平面EGM中的两条相交直线EM、GM,∴AC⊥平面EGM,∴AC⊥EG.
∵BD?平面BDF,而B1D1不在平面BDF 内,∴B1D1∥平面BDF.
取DD1的中点N,则 AH∥D1N 且AH=D1N,故AHND1为平行四边形,∴HD1∥AN.
同理可证 BF∥AN,故HD1∥BF.
∵BF?平面BDF,而HD1不在平面BDF 内,∴HD1∥平面BDF.
这样,在平面平面B1D1H 内有两条相交直线B1D1和HD1都和平面BDF平行,
∴平面BDF∥平面B1D1H.
(2)∵O为AC与BD的交点,∴BD⊥AO.再由A1A⊥平面ABCD可得 A1A⊥BD.
故BD垂直于平面平面A1AO中的两条相交直线AO和A1A,∴BD⊥平面A1AO.
而BD?平面BDF,∴平面BDF⊥平面A1AO.
(3)取CD的中点M,连接EM,GM,则EM是△CBD的中位线,∴EM∥BD,由AC⊥BD 可得 EM⊥AC.
由GM和棱A1A平行可得GM⊥平面ABCD,GM⊥AC.
这样,AC垂直于平面EGM中的两条相交直线EM、GM,∴AC⊥平面EGM,∴AC⊥EG.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目