题目内容
2.甲、乙、丙三位学生用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲及格的概率为$\frac{4}{5}$,乙及格的概率为$\frac{3}{5}$,丙及格的概率为$\frac{7}{10}$,三人各答一次,则三人中只有一人及格的概率为( )| A. | $\frac{3}{20}$ | B. | $\frac{42}{135}$ | C. | $\frac{47}{250}$ | D. | 以上都不对 |
分析 分别求出仅甲及格的概率、仅乙及格的概率、仅丙及格的概率,再把这3个概率值相加,即得所求.
解答 解:仅甲及格的概率为 $\frac{4}{5}$×$\frac{2}{5}$×$\frac{3}{10}$=$\frac{24}{250}$,仅乙及格的概率为$\frac{1}{5}$×$\frac{3}{5}$×$\frac{3}{10}$=$\frac{9}{250}$,
仅丙及格的概率为$\frac{1}{5}$×$\frac{2}{5}$×$\frac{7}{10}$=$\frac{14}{250}$,
故三人各答一次,则三人中只有一人及格的概率为 $\frac{24}{250}$+$\frac{9}{250}$+$\frac{14}{250}$=$\frac{47}{250}$,
故选:C.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下图几何体是由选项中的哪个平面图旋转而得到的( )
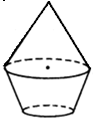

| A. | 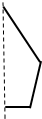 | B. | 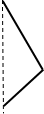 | C. | 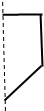 | D. |  |
12.在△ABC中,若∠B=30°,AB=2$\sqrt{3}$,AC=2,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$或$\sqrt{2}$ | C. | 2$\sqrt{3}$或$\sqrt{3}$ | D. | 2$\sqrt{3}$ |