题目内容
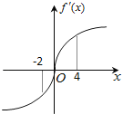
【题目】已知定义在R上的函数f（x）满足f（4）=f（﹣2）=1，f′（x）为f（x）的导函数，且导函数y=f′（x）的图象如图所示．则不等式f（x）＜1的解集是（ ）
A. （﹣2，0）
B. （﹣2，4）
C. （0，4）
D. （﹣∞，﹣2）∪（4，+∞）
【答案】B
【解析】
试题由函数y=f′（x）的图象，确定函数的单调性和单调区间，然后函数的单调性即可求不等式的解集．
解：由导函数y=f′（x）的图象可知，当x≥0时，f'（x）≥0，此时函数f（x）得到递增，
当x≤0时，f'（x）≤0，此时函数f（x）得到递减，
当x=0时，函数f（x）取得极小值，同时也是最小值，
∵f（4）=f（﹣2）=1，
∴不等式f（x）＜1的解为﹣2＜x＜4，
即不等式f（x）＜1的解集为（﹣2，4），
故选：B．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】如今我们的互联网生活日益丰富，除了可以很方便地网购，网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在
市的普及情况， 
市某调查机构借助网络进行了关于网络外卖的问卷调查，并从参与调查的网民中抽取了200人进行抽样分析，得到表格：（单位：人）
经常使用网络外卖 | 偶尔或不用网络外卖 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
（1）根据表中数据，能否在犯错误的概率不超过
的前提下认为
市使用网络外卖的情况与性别有关？
（2）①现从所抽取的女网民中利用分层抽样的方法再抽取5人，再从这5人中随机选出3人赠送外卖优惠券，求选出的3人中至少有2人经常使用网络外卖的概率；
②将频率视为概率，从
市所有参与调查的网民中随机抽取10人赠送礼品，记其中经常使用网络外卖的人数为
，求
的数学期望和方差.
参考公式： 
，其中
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】“微信运动”是一个类似计步数据库的公众账号.用户只需以运动手环或手机协处理器的运动数据为介，然后关注该公众号，就能看见自己与好友每日行走的步数，并在同一排行榜上得以体现.现随机选取朋友圈中的50人，记录了他们某一天的走路步数，并将数据整理如下：
步数/步 |
|
|
|
| 10000以上 |
男生人数/人 | 1 | 2 | 7 | 15 | 5 |
女性人数/人 | 0 | 3 | 7 | 9 | 1 |
规定：人一天行走的步数超过8000步时被系统评定为“积极性”，否则为“懈怠性”.
（1）填写下面列联表（单位：人），并根据列表判断是否有90%的把握认为“评定类型与性别有关”；
积极性 | 懈怠性 | 总计 | |
男 | |||
女 | |||
总计 |
附：
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（2）为了进一步了解“懈怠性”人群中每个人的生活习惯，从步行数在
的人群中再随机抽取3人，求选中的人中男性人数超过女性人数的概率.