题目内容
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)已知点![]() ,点
,点![]() ,O为坐标原点,函数
,O为坐标原点,函数![]() ,请判断:当
,请判断:当![]() 时
时![]() 的零点个数.
的零点个数.
【答案】(1)见解析(2)![]() 在
在![]() 上零点个数为2.
上零点个数为2.
【解析】
(1)不等式等价![]() ,设
,设![]() ,计算其导函数的最值得到函数的单调区间,计算最值得到答案.
,计算其导函数的最值得到函数的单调区间,计算最值得到答案.
(2)计算得到函数表达式,求导,讨论![]() ,
,![]() ,
,![]() ,
,![]() 四种情况,根据函数单调性分别计算零点得到答案.
四种情况,根据函数单调性分别计算零点得到答案.
(1)![]() 等价于证明
等价于证明![]() .
.
令![]() ,则
,则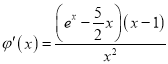 .
.
令![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
∴![]() ,
,
∴![]() 在
在![]() 上恒成立.
上恒成立.
∵![]() 在
在![]() 递减,在
递减,在![]() 递增,∴
递增,∴![]() ,∴
,∴![]() .
.
(2)点![]() ,点
,点![]() ,
,![]() ,
,
∴![]() .
.
①当![]() 时,可知
时,可知![]() ,即
,即![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() 在
在![]() 单调递减.又∵
单调递减.又∵![]() ,
,![]() .
.
∴![]() 在
在![]() 上有一个零点.
上有一个零点.
②当![]() 时,设
时,设![]() ,则
,则![]() ,函数单调递增,
,函数单调递增,
故![]() ,故
,故![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上无零点.
上无零点.
③当![]() 时,∵
时,∵![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又∵![]() ,
,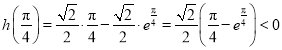 ,
,
∴![]() 在
在![]() 上存在一个零点.
上存在一个零点.
④当![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 无零点.
无零点.
综上,![]() 在
在![]() 上零点个数为2.
上零点个数为2.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目