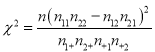题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() ,D,E分别是
,D,E分别是![]() 的中点.
的中点.
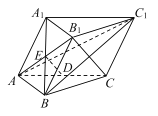
(1)求证:DE∥平面![]()
(2)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
【答案】(1)见证明;(2)见证明
【解析】
(1)连结AB1,B1C,推导出四边形ABB1A1是平行四边形,DE∥B1C,由此能证明DE∥平面BCC1B1.
(2)推导出DE∥B1C,从而AB⊥B1C,推导出平行四边形BCC1B1是菱形,从而BC1⊥B1C,再由AB⊥B1C,得BC1⊥平面ABC1,由此能证明平面ABC1⊥平面BCC1B1.
(1)连结![]() .
.
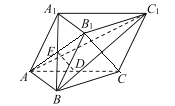
在三棱柱![]() 中,
中,![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
因为E是![]() 的中点,
的中点,
所以E也是![]() 中点,
中点,
又因为D是AC的中点,
所以![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以DE∥平面![]() .
.
(2) 由(1)知![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
在三棱柱![]() 中,
中,![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,
因为![]() ,所以
,所以![]() ,
,
所以平行四边形![]() 是菱形,
是菱形,
所以![]() ,
,
又因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |