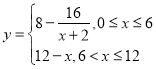题目内容
【题目】已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,对
,对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() .若正实数
.若正实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)详见解析;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)求导后,分别在![]() 和
和![]() 两种情况下根据导函数的正负求得函数的单调区间;
两种情况下根据导函数的正负求得函数的单调区间;
(2)通过分离变量得到![]() ,令
,令![]() ,利用导数可求得
,利用导数可求得![]() 最大值,由此得到
最大值,由此得到![]() ;
;
(3)设![]() ,以
,以![]() 为变量,令
为变量,令![]() ,通过判断导函数的正负可确定
,通过判断导函数的正负可确定![]() 在
在![]() 上单调递增,得到
上单调递增,得到![]() ,从而得到结论.
,从而得到结论.
(1)由题意知:![]() 定义域为
定义域为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,即
,即![]() 恒成立,
恒成立,
![]() 函数
函数![]() 的单调递增区间为
的单调递增区间为![]() ;无单调递减区间;
;无单调递减区间;
②当![]() 时,令
时,令![]() ,
,
解得:![]() ,
,![]() ,可知
,可知![]() ,
,
![]() 当
当![]() 和
和![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
![]() 的单调递增区间为
的单调递增区间为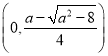 ,
,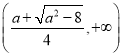 ;单调递减区间为
;单调递减区间为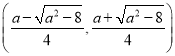 ;
;
综上所述:①当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
②当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为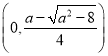 ,
,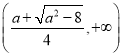 ,单调递减区间为
,单调递减区间为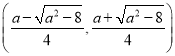 .
.
(2)![]() 对
对![]() 恒成立,即为对任意的
恒成立,即为对任意的![]() ,都有
,都有![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增;
单调递增;
当![]() ,
,![]() ,即
,即![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.
(3)证明:当![]() 时,
时,![]() ,
,
不妨设![]() ,以
,以![]() 为变量,令
为变量,令![]() ,
,
则![]()
![]() 且
且![]() ,
,
![]() ,即
,即![]() ,又
,又![]() 为增函数,
为增函数,
![]() ;
;
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
即![]() .
.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目