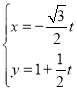Question

【题目】已知函数，g（x）＝b（x﹣1），其中a≠0，b≠0

（1）若a＝b，讨论F（x）＝f（x）﹣g（x）的单调区间；

（2）已知函数f（x）的曲线与函数g（x）的曲线有两个交点，设两个交点的横坐标分别为x1，x2，证明：．

Answer 1

【答案】（1）见解析（2）见解析

【解析】

（1）求导得，按照a＞0、 a＜0讨论的正负即可得解；

（2）设x1＞x2，转化条件得，令，，只需证明即可得证.

（1）由已知得，

∴，

当0＜x＜1时，∵1﹣x2＞0，﹣lnx＞0，∴1﹣x2﹣lnx＞0，；

当x＞1时，∵1﹣x2＜0，﹣lnx＜0，∴1﹣x2﹣lnx＜0．

故若a＞0，F（x）在（0，1）上单调递增，在（1，+∞）上单调递减；

故若a＜0，F（x）在（0，1）上单调递减，在（1，+∞）上单调递增．

（2）不妨设x1＞x2，依题意，

∴，同理得

由①﹣②得，∴，

∴，

∴，

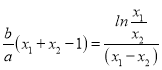故只需证，

取∴，即只需证明，成立，

即只需证，成立，

∵，

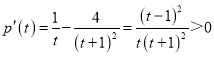∴p（t）在区间[1，+∞）上单调递增，

∴p（t）＞p（1）＝0，t＞1成立，

故原命题得证．