题目内容
【题目】已知过抛物线 ![]() 的焦点,斜率为
的焦点,斜率为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() ,
, ![]() (
( ![]() )两点,且
)两点,且 ![]() .
.
(1)求该抛物线的方程;
(2)![]() 为坐标原点,
为坐标原点, ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:设直线AB方程为:y= ![]()
联立 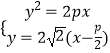 得
得 ![]()
由韦达定理得: ![]()
由抛物线定理知:
|AB|=|AF|+|BF|= ![]()
得: ![]() 即p=4
即p=4
∴抛物线方程为: ![]()
(2)解:由p=4,方程: ![]() 化为
化为 ![]()
解得x1=1, x2=4.即A(1,-2 ![]() ) B(4,4
) B(4,4 ![]() )
)
由 ![]() +
+ ![]() (4,4
(4,4 ![]() )
)
知 ![]() 代入抛物线方程
代入抛物线方程![]() .
.
解得: ![]() =0或
=0或 ![]() =2
=2
【解析】本题主要考查有关抛物线的标准方程和简单的性质问题。第一小题,主要是根据弦长问题求解抛物线的标准方程,先根据题意求出抛物线的交点坐标,进而写出过焦点的直线方程,然后和抛物线方程进行联立,利用弦长公式即可求得p,求出抛物线的标准方程。第二小题主要是抛物线性质的应用,根据第一小题中求出点A,B的坐标,根据向量的关系式 O C = O A + λ O B 求出点C的坐标,代入抛物线方程即可求解。

练习册系列答案
相关题目