题目内容
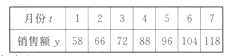
【题目】如图,在直角梯形SABC中,∠B=∠C= ![]() ,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB. 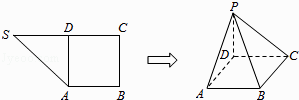
(1)求证:PD⊥平面ABCD;
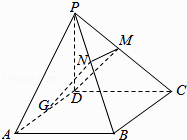
(2)已知PD=AD,PD+AD+DC=6,G是AD的中点,当线段PB取得最小值时,则在平面PBC上是否存在点F,使得FG⊥平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
【答案】
(1)证明:∵PA⊥AB,AB⊥AD,PA⊥AD=A,
∴AB⊥平面PAD,
∵PD平面PAD,
∴AB⊥PD,
∵PD⊥AD,AD∩AB=A,
∴PD⊥平面ABCD
(2)解:设PD=x,则AD=x,DC=6﹣2x,
∴PB2=x2+x2+(6﹣2x)2=6(x﹣2)2+12,当且仅当x=2时,PB2取得最小值,
即PB取得最小值,
取PC的中点M,PB的中点N,
则DM⊥平面PBC,
∵四边形DMNG是平行四边形,
∴GN∥DM,
GN⊥平面PBC,
∴在平面PBC上存在点F,即PB的中点,使FG⊥平面PBC.
【解析】(1)根据线面垂直的判定定理即可证明PD⊥平面ABCD;(2)根据线面垂直的判定定理以及直线平行的性质进行证明即可.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目