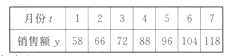
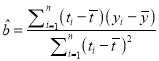题目内容
【题目】以下四个命题： ①已知随机变量X～N（0，σ2），若P（|X|＜2）=a，则P（X＞2）的值为 
；
②设a、b∈R，则“log2a＞log2b”是“2a﹣b＞1”的充分不必要条件；
③函数f（x）= 
﹣（ 
）x的零点个数为1；
④命题p：n∈N，3n≥n2+1，则￢p为n∈N，3n≤n2+1．
其中真命题的序号为 ．
【答案】②③
【解析】解：①已知随机变量X～N（0，σ2），若P（|X|＜2）=a， 则P（X＞2）= 
（1﹣P（|X|＜2））= 
，故①错；②设a、b∈R，log2a＞log2ba＞b＞0a﹣b＞02a﹣b＞1，由于a﹣b＞0，a，b不一定大于0，
则“log2a＞log2b”是“2a﹣b＞1”的充分不必要条件，故②对；③由y= 
和y=（ ）x的图象，可得它们只有一个交点，
即函数f（x）= ﹣（ ）x的零点个数为1，故③对；④命题p：n∈N，3n≥n2+1，则￢p为n∈N，3n＜n2+1．故④错．
所以答案是：②③．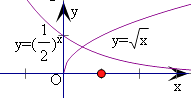
【考点精析】根据题目的已知条件，利用命题的真假判断与应用的相关知识可以得到问题的答案，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．
【题目】近年来，微信越来越受欢迎，许多人通过微信表达自己、交流思想和传递信息，微信是现代生活中进行信息交流的重要工具．而微信支付为用户带来了全新的支付体验，支付环节由此变得简便而快捷．某商场随机对商场购物的100名顾客进行统计，其中40岁以下占 
，采用微信支付的占 
，40岁以上采用微信支付的占 
．
（Ⅰ）请完成下面2×2列联表：
40岁以下 | 40岁以上 | 合计 | |
使用微信支付 | |||
未使用微信支付 | |||
合计 |
并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”？
（Ⅱ）若以频率代替概率，采用随机抽样的方法从“40岁以下”的人中抽取2人，从“40岁以上”的人中抽取1人，了解使用微信支付的情况，问至少有一人使用微信支付的概率为多少？
参考公式： 
，n=a+b+c+d．
参考数据：
P（K2≥k0） | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.760 | 3.841 | 6.635 | 10.828 |
