题目内容

已知等差数列{an}的公差d＜0，前n项的和Sn满足：S20＞0，S21＜0，那么数列{Sn}中最大的项是（　　）
A．S9B．S10C．S19D．S20
由已知等差数列{an}的公差d＜0，可得数列{an}为递减数列，
S20=
20(a1+a20)
2
=10（a1+a20）=10（a10+a11）＞0，即a10+a11＞0；
同理由S21＜0，可得S21=
21(a1+a21)
2
=
21×2a11
2
=21a11＜0，即a11＜0，
综上可得，a10＞0，a11＜0，结合数列递减的特点，
可得数列{an}的前10项都为正数，从第11项开始全为负数，因此前10项和最大．
故选B．
练习册系列答案
相关题目
设数列{an}的前n项和为Sn，且Sn=(m+1)－man 对任意正整数n都成立，其中m为常数，且m＜－1.
(1)求证:{an}是等比数列；
(2)设数列{an}的公比q=f(m)，数列{bn}满足:b1=a1,bn=f(bn－1)(n≥2,n∈N*). 试问当m为何值时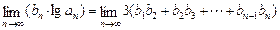，成立？
已知等差数列{an}的前n项和为Sn，若m＞1，且am-1+am+1-am2=0，S2m-1=38，则m等于（　　）
A．38B．20C．10D．9
在等差数列{an}中，a1=12，且3a8=5a13，则Sn中最大的是（　　）
A．S20B．S21C．S10D．S11
（文）等差数列{an}的前n项和为Sn，S30=12S10，S10+S30=130，则S20=（　　）
A．40B．50C．60D．70
在等差数列{an}中，a1=1，a2-a5=3，若其前n项和为Sn，则S100=______．
等差数列{an}中，a2=4，公差d=2，则a1=______，S5=______．
已知{an}为等差数列，且a3=5，a7=2a4-1．
（Ⅰ）求数列{an}的通项公式及其前n项和Sn；
（Ⅱ）若数列{bn}满足b1+4b2+9b3+…+n2bn=an求数列{bn}的通项公式．
（文）等比数列{an}的前n项和为Sn，已知S3=a2+10a1，a5=9，则a1=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网