题目内容
设数列{an}的前n项和为Sn,且Sn=(m+1)-man 对任意正整数n都成立,其中m为常数,且m<-1.
对任意正整数n都成立,其中m为常数,且m<-1.
(1)求证:{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足:b1= a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,
a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,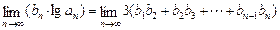 成立?
成立?
 对任意正整数n都成立,其中m为常数,且m<-1.
对任意正整数n都成立,其中m为常数,且m<-1.(1)求证:{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足:b1=
 a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,
a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,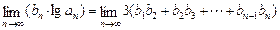 成立?
成立?(1) 证明略,(2) 

(1)由已知Sn+1=(m+1)-man+1 ①, Sn=(m+1)-man ②,
由①-②,得an+1=man-man+1,即(m+1)an+1=man对任意正整数n都成立.
∵m为常数,且m<-1
∴ ,即{
,即{ }为等比数列.
}为等比数列.
(2)当n=1时,a1=m+1-ma1,∴a1=1,从而b1=

由(1)知q=f(m)= ,∴bn=f(bn-1)=
,∴bn=f(bn-1)= (n∈N*,且n≥2)
(n∈N*,且n≥2)
∴ ,即
,即 ,
,
∴{ }为等差数列。 ∴
}为等差数列。 ∴ =3+(n-1)=n+2,
=3+(n-1)=n+2,
 (n∈N*).
(n∈N*).


 .
.
由①-②,得an+1=man-man+1,即(m+1)an+1=man对任意正整数n都成立.
∵m为常数,且m<-1
∴
 ,即{
,即{ }为等比数列.
}为等比数列.(2)当n=1时,a1=m+1-ma1,∴a1=1,从而b1=


由(1)知q=f(m)=
 ,∴bn=f(bn-1)=
,∴bn=f(bn-1)= (n∈N*,且n≥2)
(n∈N*,且n≥2)∴
 ,即
,即 ,
,∴{
 }为等差数列。 ∴
}为等差数列。 ∴ =3+(n-1)=n+2,
=3+(n-1)=n+2, (n∈N*).
(n∈N*).

 .
.
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,an+an+1=
,an+an+1= ,则
,则 (a1+a2+…+an) = ( )
(a1+a2+…+an) = ( )
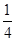

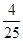
 B
B  C
C  D
D 
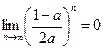 ,则a的取值范围是( )
,则a的取值范围是( )
 或
或

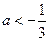 或
或
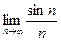 =0,则极限
=0,则极限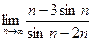 =_______________。
=_______________。 的公差
的公差 是2,前
是2,前 项的和为
项的和为 则
则
 .
. 的值为( )
的值为( ) .
. D.1
D.1