Question

【题目】双曲线 =1（a＞0，b＞0）的右焦点为F，直线y= x与双曲线相交于A、B两点．若AF⊥BF，则双曲线的渐近线方程为 ．

Answer 1

【答案】y=±2x
【解析】解：由题意可知：双曲线 =1（a＞0，b＞0）焦点在x轴上，右焦点F（c，0），
则 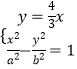，整理得：（9b2﹣16a2）x2=9a2b2 ， 即x2= ，
∴A与B关于原点对称，设A（x， x），B（﹣x，﹣ x），
=（x﹣c， x）， =（﹣x﹣c，﹣ x），
∵AF⊥BF，
∴ =0，即（x﹣c）（﹣x﹣c）+ x×（﹣ x）=0，
整理得：c2= x2 ，
∴a2+b2= × ，即9b4﹣32a2b2﹣16a4=0，
∴（b2﹣4a2）（9b2+4a2）=0，
∵a＞0，b＞0，
∴9b2+4a2≠0，
∴b2﹣4a2=0，
故b=2a，
双曲线的渐近线方程y=± x=±2x，
所以答案是：y=±2x．