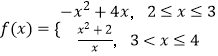题目内容
【题目】函数f(x)=log3(x2+2x﹣8)的定义域为A,函数g(x)=x2+(m+1)x+m.
(1)若m=﹣4时,g(x)≤0的解集为B,求A∩B;
(2)若存在 ![]() 使得不等式g(x)≤﹣1成立,求实数m的取值范围.
使得不等式g(x)≤﹣1成立,求实数m的取值范围.
【答案】
(1)解:由x2+2x﹣8>0,解得:x∈(﹣∞,﹣4)∪(2,+∞),
故则函数f(x)=log3(x2+2x﹣8)的定义域A=(﹣∞,﹣4)∪(2,+∞),
若m=﹣4,g(x)=x2﹣3x﹣4,由x2﹣3x﹣4≤0,解得:x∈[﹣1,4],则B=[﹣1,4]
所以A∩B=(2,4]
(2)解:存在 ![]() 使得不等式x2+(m+1)x+m≤﹣1成立,
使得不等式x2+(m+1)x+m≤﹣1成立,
即存在 ![]() 使得不等式﹣m≥
使得不等式﹣m≥ ![]() 成立,所以﹣m≥(
成立,所以﹣m≥( ![]() )min
)min
因为 ![]() =x+1+
=x+1+ ![]() ﹣1≥1,
﹣1≥1,
当且仅当x+1=1,即x=0时取得等号
所以﹣m≥1,
解得:m≤﹣1
【解析】(1)求出集合A,B,由交集运算的定义,可得A∩B;(2)若存在 ![]() 使得不等式g(x)≤﹣1成立,即存在
使得不等式g(x)≤﹣1成立,即存在 ![]() 使得不等式﹣m≥
使得不等式﹣m≥ ![]() 成立,所以﹣m≥(
成立,所以﹣m≥( ![]() )min , 解得实数m的取值范围.
)min , 解得实数m的取值范围.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

 阅读快车系列答案
阅读快车系列答案【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取顺序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产
过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地
变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就认为这条生产线在这一天
+3s)之外的零件,就认为这条生产线在这一天
的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=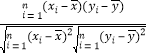 ,
,![]() ≈0.09.
≈0.09.
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为6
之间是正相关还是负相关;若该地1月份某天的最低气温为6![]() ,请用所求回归方程预测该店当日的营业额.
,请用所求回归方程预测该店当日的营业额.
附: 回归方程![]() 中,
中,  ,
,![]()
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
分类 | 积极参加 班级工作 | 不太主动参 加班级工作 | 总计 |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
总计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关,并说明理由.