题目内容
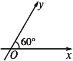
【题目】如图所示,在平面斜坐标系xOy中,∠xOy=60°,平面上任意一点P关于斜坐标系的斜坐标是这样定义的:若
=xe1+ye2(其中e1,e2分别为x轴、y轴同方向的单位向量),则点P的斜坐标为(x,y).
(1)若点P在斜坐标系xOy中的斜坐标为(2,-2),求点P到原点O的距离.
(2)求以原点O为圆心,1为半径的圆在斜坐标系xOy中的方程.
【答案】（1）2；（2）
【解析】
(1)先根据点P的斜坐标得到
=2e1-2e2, 再平方求出||2=4，即点P到原点O的距离为2.（2）设圆上动点M的斜坐标为(x,y),
=xe1+ye2,再平方化简得所求圆的方程为x2+y2+xy=1.
(1)因为点P的斜坐标为(2,-2), 所以=2e1-2e2,
所以||2=(2e1-2e2)2=4
-8e1·e2+4
=8-8×1×1×cos 60°=8-4=4,所以||=2,即点P到原点O的距离为2.
(2)设圆上动点M的斜坐标为(x,y),
则=xe1+ye2,所以(xe1+ye2)2=1,
则x2+2xye1·e2+y2=1,即x2+y2+xy=1,
故所求圆的方程为x2+y2+xy=1.
练习册系列答案
特高级教师点拨系列答案
相关题目
【题目】如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（
吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
（1）请根据表中提供的数据，用最小二乘法求出
关于
的线性回归方程
；
（2）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考：用最小二乘法求线性回归方程系数公式
， 
）