题目内容
【题目】已知椭圆C: ![]() (a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,椭圆C上任意一点到椭圆左右两个焦点的距离之和为4.
(a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,椭圆C上任意一点到椭圆左右两个焦点的距离之和为4.
(1)求椭圆C的方程;
(2)椭圆C与X轴负半轴交于点A,直线过定点(﹣1,0)交椭圆于M,N两点,求△AMN面积的最大值.
【答案】
(1)解:由题意a=2b,
又2a=4,所以a=2,b=1
椭圆方程为 ![]()
(2)解:A点坐标为(﹣2,0),直线MN过定点(﹣1,0),
∴令直线MN的方程为x=my﹣1,
联立 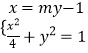 ,消去x得(m2+4)y2﹣2my﹣3=0,
,消去x得(m2+4)y2﹣2my﹣3=0,
∴ ![]() ,
, ![]() ,
,
![]()
= ![]() =
= ![]() ,
,
令t=m2+3,t≥3,
∴ ![]() ,
,
当且仅当t=m2+3=3即m=0时,△AMN面积的最大值为 ![]()
【解析】(1)由题意a=2b,根据椭圆C上任意一点到椭圆左右两个焦点的距离之和为4,利用椭圆的定义求出a,可得b,即可求椭圆C的方程;(2)设直线MN:x=my﹣1,联立椭圆方程,消去x,运用韦达定理,再由△AMN面积为S= ![]() |AD||y1﹣y2|,代入化简整理,再由对勾函数的性质,即可得到最大值.
|AD||y1﹣y2|,代入化简整理,再由对勾函数的性质,即可得到最大值.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目