题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求证:
,求证:![]() .
.
【答案】(1)1(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(Ⅰ)首先求函数的导数![]() ,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式
,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式![]() 等价于
等价于![]() ,根据导数分别求两个函数的最小值和最大值,建立不等式求
,根据导数分别求两个函数的最小值和最大值,建立不等式求![]() 的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即
的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即![]() ,证明
,证明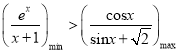 ,求
,求![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数![]() 在
在![]() 上的零点的个数为1,,
上的零点的个数为1,,
理由如下:因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以函数![]() 在
在![]() 上是单调递增函数.
上是单调递增函数.
因为![]() ,
,![]() ,
,
根据函数零点存在性定理得
函数![]() 在
在![]() 上的零点的个数为1.
上的零点的个数为1.
(Ⅱ)因为不等式![]() 等价于
等价于![]() ,
,
所以![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,等价于
成立,等价于![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 时,
时,![]() 取得最小值-1,
取得最小值-1,
又![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因此,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
所以![]() ,所以
,所以![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,要证
时,要证![]() ,只要证
,只要证![]() ,
,
只要证![]()
![]() ,
,
只要证![]() ,
,
由于![]() ,
,![]() 只要证
只要证![]() .
.
下面证明![]() 时,不等式
时,不等式![]() 成立.
成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是单调递减;
是单调递减;
当![]() 时,
时,![]() ,
,![]() 是单调递增.
是单调递增.
所以当且仅当![]() 时,
时,![]() 取得极小值也就是最小值为1.
取得极小值也就是最小值为1.
令![]() ,其可看作点
,其可看作点![]() 与点
与点![]() 连线的斜率,
连线的斜率,
所以直线![]() 的方程为:
的方程为:![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以直线
上,所以直线![]() 与圆
与圆![]() 相交或相切,
相交或相切,
当直线![]() 与圆
与圆![]() 相切且切点在第二象限时,
相切且切点在第二象限时,
当直线![]() 取得斜率
取得斜率![]() 的最大值为1.
的最大值为1.
故![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
综上所述,当![]() 时,
时,![]() 成立.
成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
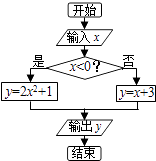
小学生10分钟应用题系列答案【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生. 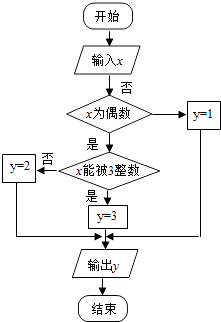
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.