题目内容
【题目】已知椭圆
的左、右焦点
，
，离心率
，短轴长为2.
（Ⅰ）求椭圆的方程；
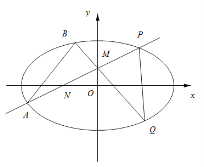
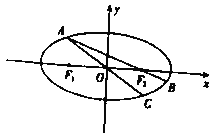
（Ⅱ）如图，点
为椭圆上一动点（非长轴端点），
的延长线于椭圆交于
点，
的延长线于椭圆交于
点，求
面积的最大值
【答案】（1）
; （2）
.
【解析】【试题分析】（１）依据题设建立方程组进行求解；（２）依据题设条件运用直线与椭圆的位置关系建立三角形面积的目标函数，运用不等式求得其最值从而使得问题获解。
（1）椭圆
中，
过其中两个端点的直线斜率为
，∴
①，
过两个焦点和一个顶点的三角形面积为1，∴
②；
又
③，
用①②③解得
，
；
∴椭圆的方程为.
（2）当直线
的斜率不存在时，
可知
，
，
，
故
，
当直线的斜率存在时，设直线的方程为
，
联立方程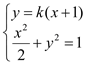
化简得，
，
∴
，
，
故
，
，
故
，
点
到直线的距离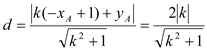
，
故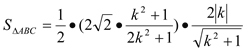
；
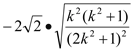
综上，
的面积的最大值为.
练习册系列答案
特高级教师点拨系列答案
相关题目
