题目内容
已知命题p：?x∈R，x2-ax+1≥0，命题q：?x＞0，x2-ax+1≤0，若p∧q为真，求a的值．
∵?x∈R，x2-ax+1≥0，
则△=a2-4≤0⇒-2≤a≤2，
∴命题p为真时，-2≤a≤2；
∵?x＞0，x2-ax+1≤0，
则△=a2-4≥0⇒a≥2或a≤-2，
∴命题q为真时，a≥2或a≤-2．
由复合命题真值表知：若p∧q为真，命题p、q均为真，
∴a=2或-2．
则△=a2-4≤0⇒-2≤a≤2，
∴命题p为真时，-2≤a≤2；
∵?x＞0，x2-ax+1≤0，
则△=a2-4≥0⇒a≥2或a≤-2，
∴命题q为真时，a≥2或a≤-2．
由复合命题真值表知：若p∧q为真，命题p、q均为真，
∴a=2或-2．
练习册系列答案
名校课堂系列答案
相关题目
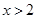”是“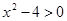
”的 条件（在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个填空）.
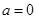”是复数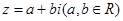
为纯虚数的 条件.（填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）
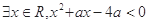”为假命题，是“
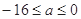”的( ).