题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形且
是直角梯形且![]() ∥
∥![]() ,侧面
,侧面![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() .
.
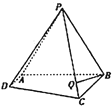
(1)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小;
所成的锐二面角的大小;
(2)若![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)分别取![]() 的中点为
的中点为![]() ,易得
,易得![]() 两两垂直,以
两两垂直,以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,易得
轴建立空间直角坐标系,易得![]() 为平面
为平面![]() 的法向量,只需求出平面
的法向量,只需求出平面![]() 的法向量为
的法向量为![]() ,再利用
,再利用![]() 计算即可;
计算即可;
(2)求出![]() ,利用
,利用![]() 计算即可.
计算即可.
(1)分别取![]() 的中点为
的中点为![]() ,连结
,连结![]() .
.
因为![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]() .
.
因为![]() ,所以
,所以![]() .
.
因为侧面![]() 为等边三角形,
为等边三角形,
所以![]()
又因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 两两垂直.
两两垂直.
以![]() 为空间坐标系的原点,分别以
为空间坐标系的原点,分别以![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
因为![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则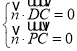 ,即
,即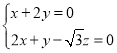 .
.
取![]() ,则
,则![]() ,所以
,所以![]() .
.
又![]() 为平面
为平面![]() 的法向量,设平面
的法向量,设平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,则
,则
![]() ,
,
所以平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() .
.

(2)由(1)得,平面![]() 的法向量为
的法向量为![]() ,
,
所以成![]() .
.
又直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以![]() ,即
,即![]() ,
,
即![]() ,
,
化简得![]() ,所以
,所以![]() ,符合题意.
,符合题意.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】我校随机抽取100名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 总计 | |
学习积极性高 | 40 | ||
学习积极性一般 | 30 | ||
总计 | 100 |
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法学生的学习积极性与对待班级工作的态度是否有关?并说明理由.附:
| 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
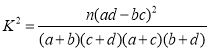
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: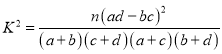 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |