题目内容
【题目】已知抛物线![]() 的焦点坐标为
的焦点坐标为![]()
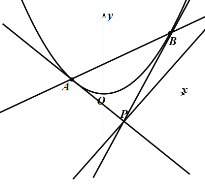
(1)求抛物线方程;
(2)过直线![]() 上一点
上一点![]() 作抛物线的切线切点为A,B
作抛物线的切线切点为A,B
①设直线PA、AB、PB的斜率分别为![]() ,求证:
,求证:![]() 成等差数列;
成等差数列;
②若以切点B为圆心r为半径的圆与抛物线C交于D,E两点且D,E关于直线AB对称,求点P横坐标的取值范围.
【答案】(1)![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() .
.
【解析】
(1)根据焦点求出p即可写出抛物线方程;(2)①设![]() ,利用导数的几何意义用
,利用导数的几何意义用![]() 、
、![]() 表示出
表示出![]() 、
、![]() ,再用
,再用![]() 、
、![]() 表示出
表示出![]() ,由
,由![]() 即可证明;②求出直线AP、直线BP的方程,联立求出两直线的交点坐标P,由点P在直线
即可证明;②求出直线AP、直线BP的方程,联立求出两直线的交点坐标P,由点P在直线![]() 上进一步化简直线AP的方程,联立抛物线方程与直线DE的方程得到关于x的一元二次方程,根据题意
上进一步化简直线AP的方程,联立抛物线方程与直线DE的方程得到关于x的一元二次方程,根据题意![]() ,再由点H在直线AB上将不等式转化为关于t的不等式求解即可.
,再由点H在直线AB上将不等式转化为关于t的不等式求解即可.
(1)由题意知![]() ,
,![]() ,抛物线方程为
,抛物线方程为![]() ;
;
(2)①设![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
则![]() ,
,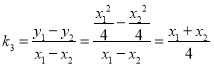 ,
,
所以![]() ,即
,即![]() 成等差数列.
成等差数列.
②直线AP的方程为![]() ,
,
同理直线BP的方程为![]() ,
,
则两直线的交点坐标![]() ,
,
代入直线![]() ,得
,得![]() ①,
①,
直线AB的方程为![]() ,
,
①式代入上式可得![]() ,
,
因为![]() ,所以直线AB的方程为
,所以直线AB的方程为![]() ,
,
1)若![]() 则抛物线
则抛物线![]() 上不存在两点关于直线AB对称,
上不存在两点关于直线AB对称,
2)若![]() ,设
,设![]() 为抛物线上关于直线AB对称的两点,
为抛物线上关于直线AB对称的两点,
此时![]()
设DE方程为![]() ,DE与直线AB交于点
,DE与直线AB交于点![]() ,
,
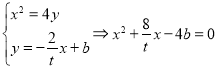 ,
,
![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为H点在直线AB上,
所以![]() 代入
代入![]() 式得
式得![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目