题目内容
【题目】对于直线![]() 与抛物线
与抛物线![]() ,若
,若![]() 与
与![]() 有且只有一个公共点且
有且只有一个公共点且![]() 与
与![]() 的对称轴不平行(或重合),则称
的对称轴不平行(或重合),则称![]() 与
与![]() 相切,直线
相切,直线![]() 叫做抛物线
叫做抛物线![]() 的切线.
的切线.
(1)已知![]() 是抛物线上一点,求证:过点
是抛物线上一点,求证:过点![]() 的
的![]() 的切线
的切线![]() 的斜率
的斜率![]() ;
;
(2)已知![]() 为
为![]() 轴下方一点,过
轴下方一点,过![]() 引抛物线的切线,切点分别为
引抛物线的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() 成等差数列;
成等差数列;
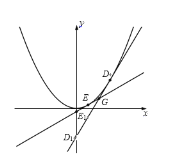
(3)如图所示,![]() 、
、![]() 是抛物线
是抛物线![]() 上异于坐标原点的两个不同的点,过点
上异于坐标原点的两个不同的点,过点![]() 的
的![]() 的切线分别是
的切线分别是![]() ,直线
,直线![]() 交于点
交于点![]() ,且与
,且与![]() 轴分别交于点
轴分别交于点![]() .设
.设![]() 为方程
为方程![]() 的两个实根,
的两个实根,![]() 表示实数
表示实数![]() 中较大的值.求证:“点
中较大的值.求证:“点![]() 在线段
在线段![]() 上”的充要条件是“
上”的充要条件是“![]() ”.
”.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析;
【解析】
(1)将抛物线方程变为![]() ,利用导数的几何意义证得结论;
,利用导数的几何意义证得结论;
(2)利用点斜式写出直线![]() ,联立可求得交点横坐标为
,联立可求得交点横坐标为![]() ,即
,即![]() ,证得结论;
,证得结论;
(3)首先联立![]() 方程,可求得
方程,可求得![]() 点坐标,进而得到
点坐标,进而得到![]() 的值;
的值;
①当![]() 在
在![]() 上时,由
上时,由![]() 可求得
可求得![]() ,进而必要性可证得;
,进而必要性可证得;
②当![]() ,可得
,可得![]() ,进而
,进而![]() ,充分性可证得;
,充分性可证得;
由此可总结出结论.
(1)将抛物线方程变为:![]()
![]()
当![]() 时,
时,![]() ,即切线
,即切线![]() 的斜率
的斜率![]()
(2)由(1)知,直线![]() ;直线
;直线![]()
由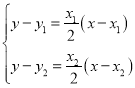 得:
得:![]()
又![]() ,
,![]()
![]()
![]()
![]()
![]() 为直线
为直线![]() 交点
交点 ![]()
![]() 成等差数列
成等差数列
(3)![]() 在抛物线上
在抛物线上 ![]()
由(1)知:![]()
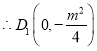
同理可得:![]()
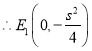
联立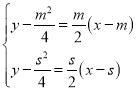 ,解得:
,解得:![]() ,
,![]() ,即
,即![]()
![]() 方程
方程![]() 两根为
两根为![]() ,
,![]()
必要性:当点![]() 在线段
在线段![]() 上时,
上时,![]()
即![]()
![]()
![]()
充分性:当![]() 时,
时,![]()
![]()
![]() ,即
,即![]()
![]() 在线段
在线段![]() 上
上
综上所述:“点![]() 在线段
在线段![]() 上”的充要条件是“
上”的充要条件是“![]() ”
”

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目