题目内容
空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面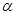 ,
,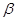 ,
,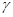 两两互相垂直,点
两两互相垂直,点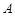 ∈
∈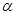 ,点
,点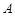 到
到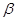 ,
,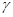 的距离都是
的距离都是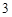 ,点
,点 是
是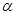 上的动点,满足
上的动点,满足 到
到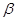 的距离是到
的距离是到 到点
到点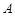 距离的
距离的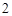 倍,则点
倍,则点 的轨迹上的点到
的轨迹上的点到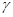 的距离的最小值是
的距离的最小值是
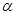 ,
,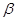 ,
,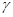 两两互相垂直,点
两两互相垂直,点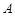 ∈
∈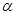 ,点
,点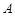 到
到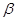 ,
,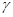 的距离都是
的距离都是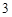 ,点
,点 是
是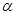 上的动点,满足
上的动点,满足 到
到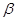 的距离是到
的距离是到 到点
到点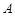 距离的
距离的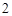 倍,则点
倍,则点 的轨迹上的点到
的轨迹上的点到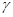 的距离的最小值是
的距离的最小值是A.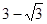 | B.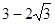 |
C.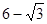 | D.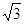 |
A
分析:原题等价于在直角坐标系中,点A(3,3),P第一象限内的动点,满足P到Y轴的距离是到P到点A 距离的2倍,则点P的轨迹上的点到x轴的距离的最小值是多少.
解:设P(x,y),
P的轨迹方程为x=2
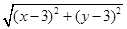 ,
,x2=4(x-3)2+4(y-3)2,
(y-3)2=
 [x2-4(x-3)2]-
[x2-4(x-3)2]- 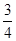 x2+6x-9,
x2+6x-9,当x=4时,最大值为3
∵(y-3)2=3,∴y=3+
 ,或y=3-
,或y=3-
∴点P 的轨迹上的点到γ 的距离的最小值是3-
 .
.故选A.

练习册系列答案
相关题目
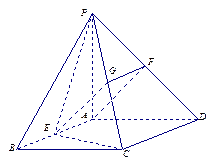
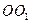 内有一个三棱柱
内有一个三棱柱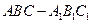 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱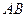 是圆
是圆 的直径。
的直径。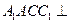 平面
平面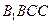 ;
;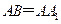 ,在圆
,在圆 柱
柱 。
。 在圆周上运动时,求
在圆周上运动时,求 与平面
与平面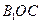 所成的角为
所成的角为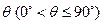 。当
。当
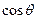 的值。
的值。
 四面体
四面体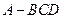 中,共顶点
中,共顶点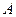 的三条棱两两互相垂直,且
的三条棱两两互相垂直,且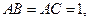 ,
,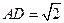 若四
若四 面体的四个顶点在一个球面上,则B,D的球面距离为_ ___ __。
面体的四个顶点在一个球面上,则B,D的球面距离为_ ___ __。 
 点,那么这两个切点在球面上的最短距离是 。
点,那么这两个切点在球面上的最短距离是 。 中
中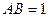 ,
,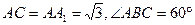
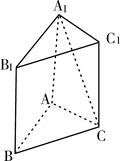
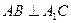
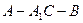 的大小
的大小