题目内容
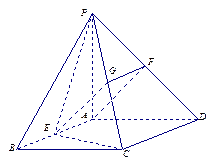
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=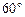 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
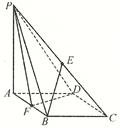
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
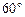 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
⑴略;⑵略;⑶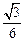
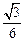
(1)取PD的中点为M,连结ME,MF,因为E是PC的中点,所以ME是△PCD的中位线.所以ME∥CD,ME=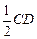 .又因为F是AB的中点,且由于ABCD是菱形,AB∥CD,AB=CD,所以ME∥FB,且ME=FB.所以四边形MEBF是平行四边形,所以BE∥MF.
.又因为F是AB的中点,且由于ABCD是菱形,AB∥CD,AB=CD,所以ME∥FB,且ME=FB.所以四边形MEBF是平行四边形,所以BE∥MF.
连结BD,因为BE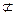 平面PDF,MF
平面PDF,MF 平面PDF,所以BE∥平面PDF.
平面PDF,所以BE∥平面PDF.
(2)因为PA⊥平面ABCD,DF 平面ABCD,所以DF⊥PA.
平面ABCD,所以DF⊥PA.
连结BD,因为底面ABCD是菱形,∠BAD=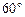 ,所以△DAB为正三角形.
,所以△DAB为正三角形.
因为F是AB的中点,所以DF⊥AB.
因为PA,AB是平面PAB内的两条相交直线,所以DF⊥平面PAB.
因为DF 平面PDF,所以平面PDF⊥平面PAB.
平面PDF,所以平面PDF⊥平面PAB.
(3)因为E是PC的中点,所以点P到平面EFD的距离与点C到平面EFD的距离相等,故 =
=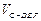 =
=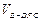 ,又
,又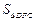 =
= ×2×
×2× =
= ,E到平面DFC的距离h=
,E到平面DFC的距离h=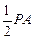 =
= ,所以
,所以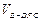 =
= ×
× ×
× =
=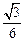 .
.
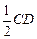 .又因为F是AB的中点,且由于ABCD是菱形,AB∥CD,AB=CD,所以ME∥FB,且ME=FB.所以四边形MEBF是平行四边形,所以BE∥MF.
.又因为F是AB的中点,且由于ABCD是菱形,AB∥CD,AB=CD,所以ME∥FB,且ME=FB.所以四边形MEBF是平行四边形,所以BE∥MF.连结BD,因为BE
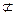 平面PDF,MF
平面PDF,MF 平面PDF,所以BE∥平面PDF.
平面PDF,所以BE∥平面PDF.(2)因为PA⊥平面ABCD,DF
 平面ABCD,所以DF⊥PA.
平面ABCD,所以DF⊥PA.连结BD,因为底面ABCD是菱形,∠BAD=
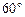 ,所以△DAB为正三角形.
,所以△DAB为正三角形.因为F是AB的中点,所以DF⊥AB.
因为PA,AB是平面PAB内的两条相交直线,所以DF⊥平面PAB.
因为DF
 平面PDF,所以平面PDF⊥平面PAB.
平面PDF,所以平面PDF⊥平面PAB.(3)因为E是PC的中点,所以点P到平面EFD的距离与点C到平面EFD的距离相等,故
 =
=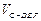 =
=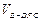 ,又
,又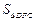 =
= ×2×
×2× =
= ,E到平面DFC的距离h=
,E到平面DFC的距离h=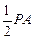 =
= ,所以
,所以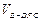 =
= ×
× ×
× =
=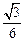 .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
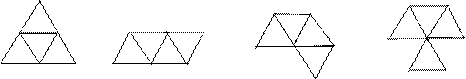
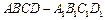 中,E、F、G分别为
中,E、F、G分别为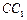 、
、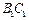 、
、 的中点,O为
的中点,O为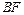 与
与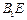 的交点,
的交点,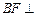 面
面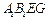
 与平面
与平面
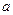 的正方体
的正方体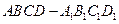 中,
中,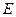 是线段
是线段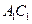 的中点,
的中点,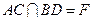 .
.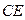 ^
^ ;
;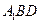 ;
;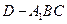 的体积.
的体积.