题目内容
4.已知⊙O的圆心为原点,与直线3x+4y-15=0相切,⊙M的方程为(x-3)2+(y-4)2=1,过⊙M上任一点P作⊙O的切线PA,切点为A,若直线PA与⊙M的另一交点为Q,当弦PQ最大时,则PA的直线方程为x=3或7x-24y+75=0.分析 利用⊙O的圆心为原点,与直线3x+4y-15=0相切,求出圆的半径,从而可得⊙O的方程;当直线PA过圆M的圆心(3,4)时,弦PQ最大,从而可设直线PA的方程,利用PA与圆O相切,可得圆心(0,0)到直线PA的距离为3,进而可求直线PA的方程.
解答 解:∵⊙O的圆心为原点,与直线3x+4y-15=0相切
∴圆心到直线的距离等于半径r=3
∴⊙O的方程为x2+y2=9
由题可知当直线PA过圆M的圆心(3,4)时,弦PQ最大
直线PA的斜率不存在时,直线x=3,满足题意;
直线PA的斜率存在时,设直线PA的方程为:y-4=k(x-3)
又因为PA与圆O相切,所以圆心(0,0)到直线PA的距离为3
即$\frac{|-3k+4|}{\sqrt{{k}^{2}+1}}$=3,可得k=$\frac{7}{24}$,
∴直线PA的方程为7x-24y+75=0
综上,直线PA的方程为x=3或7x-24y+75=0
点评 本题考查圆的方程,考查直线与圆的位置关系,利用直线与圆相切,圆心到直线的距离等于半径是解题的关键.

练习册系列答案
相关题目
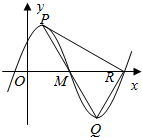 如图是函数f(x)=Asin(ωx+φ)的部分图象,P、Q分别为该图象的最高点和最低点,R是该图象与x轴的一个交点,且PR⊥QR,△PQR的面积为2$\sqrt{3}$,则函数f(x)的最小正周期为4.
如图是函数f(x)=Asin(ωx+φ)的部分图象,P、Q分别为该图象的最高点和最低点,R是该图象与x轴的一个交点,且PR⊥QR,△PQR的面积为2$\sqrt{3}$,则函数f(x)的最小正周期为4.