题目内容
7．过点P（1，2）的直线l与圆C：x2+（y-1）2=4交于A，B两点，当∠ACB最小时，直线L的方程为（ ）| A． | 2x-y=0 | B． | x-y+1=0 | C． | x+y-3=0 | D． | x=1 |
分析 利用当∠ACB最小时，CP和AB垂直，求出AB直线的斜率，用点斜式求得直线l的方程．
解答 解：圆C：x2+（y-1）2=4的圆心为C（0，1），
当∠ACB最小时，CP和AB垂直，∴AB直线的斜率等于-$\frac{1-0}{2-1}$=-1，
用点斜式写出直线l的方程为y-2=-（x-1），即x+y-3=0，
故选：C．
点评 本题考查用点斜式求直线方程的方法，两直线垂直，斜率之积等于-1．判断当∠ACB最小时，CP和AB垂直是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
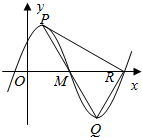如图是函数f（x）=Asin（ωx+φ）的部分图象，P、Q分别为该图象的最高点和最低点，R是该图象与x轴的一个交点，且PR⊥QR，△PQR的面积为2$\sqrt{3}$，则函数f（x）的最小正周期为4．