Question

【题目】某环线地铁按内、外环线同时运行，内、外环线的长均为30千米（忽略内、外环线长度差异）．

（1）当9列列车同时在内环线上运行时，要使内环线乘客最长候车时间为10分钟，求内环线列车的最小平均速度；

（2）新调整的方案要求内环线列车平均速度为25千米/小时，外环线列车平均速度为30千米/小时．现内、外环线共有18列列车全部投入运行，要使内外环线乘客的最长候车时间之差不超过1分钟，向内、外环线应各投入几列列车运行？

Answer 1

【答案】（1）20千米/小时；（2）内环线投入10列列车运行，外环线投入8列列车.

【解析】

（1）设内环线列车的平均速度为v千米/小时，根据内环线乘客最长候车时间为10分钟，可得，从而可求内环线列车的最小平均速度；（2）设内环线投入x列列车运行，则外环线投入（18﹣x）列列车运行，分别求出内、外环线乘客最长候车时间，，根据，解不等式，即可求得结论．

（1）设内环线列车的平均速度为v千米/小时，则要使内环线乘客最长候车时间为10分钟，可得

∴v≥20

∴要使内环线乘客最长候车时间为10分钟，内环线列车的最小平均速度是20千米/小时；

（2）设内环线投入x列列车运行，则外环线投入（18﹣x）列列车运行，内、外环线乘客最长候车时间分别为t1，t2分钟，

则，

∴

∴

∴

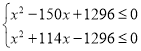
∵x∈N+，∴x＝10

∴当内环线投入10列列车运行，外环线投入8列列车时，内外环线乘客的最长候车时间之差不超过1分钟．