题目内容
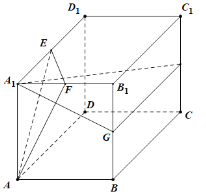
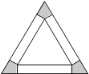
【题目】把边长为a的等边三角形铁皮剪去三个相同的四边形（如图阴影部分）后，用剩余部分做成一个无盖的正三棱柱形容器(不计接缝)，设容器的高为x，容积为
.
（1）写出函数的解析式，并求出函数的定义域；
（2）求当x为多少时，容器的容积最大？并求出最大容积.
【答案】（1）
；函数的定义域为
（2）当正三棱柱形容器高为
时，容器的容积最大为
【解析】
（1）根据棱柱的体积公式进行求解即可；
（2）利用导数求出函数
的最大值即可.
（1）因为容器的高为x，则作成的正三棱柱形容器的底边长为
则.函数的定义域为.
（2）在开区间内，
令
，即令
，解得
（舍）.
因为
在区间内，
可能是极值点.当
时，
；
当
时，
.
因此是极大值点，且在区间内，是唯一的极值点，所以
是的最大值点，并且最大值
即当正三棱柱形容器高为时，容器的容积最大为.
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
【题目】某房地产公司新建小区有A、B两种户型住宅，其中A户型住宅每套面积为100平方米，B户型住宅每套面积为80平方米，该公司准备从两种户型住宅中各拿出12套销售给内部员工，表是这24套住宅每平方米的销售价格：（单位：万元平方米）：
房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
（1）根据表格数据，完成下列茎叶图，并分别求出A，B两类户型住宅每平方米销售价格的中位数；
A户型 | B户型 | |
2. | ||
3. | ||
4. |
（2）该公司决定对上述24套住房通过抽签方式销售，购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号，每位购房者只有一次抽签机会，小明是第一位抽签的员工，经测算其购买能力最多为320万元，抽签后所抽得住房价格在其购买能力范围内则确定购买，否则，将放弃此次购房资格，为了使其购房成功的概率更大，他应该选择哪一种户型抽签？
