题目内容
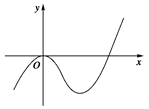
设函数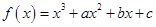 的图象如图所示,且与
的图象如图所示,且与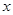 轴相切于原点,若函数的极小值为-4.
轴相切于原点,若函数的极小值为-4.
(1)求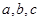 的值;
的值;
(2)求函数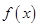 的递减区间.
的递减区间.
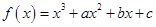 的图象如图所示,且与
的图象如图所示,且与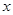 轴相切于原点,若函数的极小值为-4.
轴相切于原点,若函数的极小值为-4.
(1)求
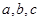 的值;
的值;(2)求函数
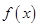 的递减区间.
的递减区间.(1)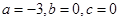
(2)单调递减区间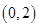
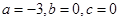
(2)单调递减区间
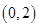
试题分析:(1)解:(1)由题意知f(0)=0,∴c=0,∴f(x)=x3+ax2+bx f'(x)=3x2+2ax+b,又∵f'(x)=b=0,∴f'(x)=3x2+2ax=0,故极小值点为x=-
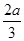
,∴f(-
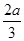 )=-4∴a=-3,(2)令f'(x)<0 即:3x2-6x<0,解得:0<x<2
)=-4∴a=-3,(2)令f'(x)<0 即:3x2-6x<0,解得:0<x<2∴函数的递减区间为(0,2)
点评:本题考查了导数的几何意义及利用导数求函数的单调区间,要注意从图象中得到有价值的结论,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
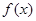 =
=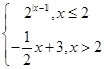 ,若互不相等的实数
,若互不相等的实数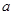 、
、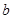 、
、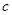 满足
满足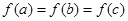 ,则
,则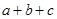 的取值范围是
的取值范围是 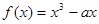 在
在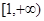 上是单调递增函数,则
上是单调递增函数,则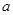 的取值范围是_____________。
的取值范围是_____________。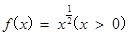 ,若对于任意
,若对于任意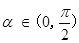 ,都有
,都有 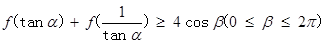 成立,则
成立,则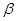 的取值范围是
的取值范围是 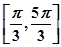
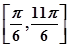
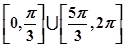
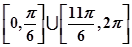
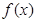 (
(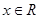 )满足
)满足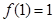 ,且
,且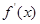 <
<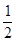 ,则
,则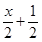 的解集为( )
的解集为( )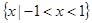
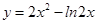 的的单调递减区间是 .
的的单调递减区间是 .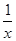 在(0,1)上是减函数.
在(0,1)上是减函数.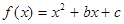 ,且
,且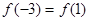 .则( )
.则( )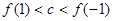
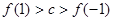

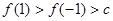
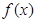 在R上是单调函数,且满足对任意
在R上是单调函数,且满足对任意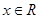 ,都有
,都有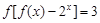 ,若则
,若则 的值是( )
的值是( )