题目内容
已知函数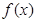 (
(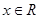 )满足
)满足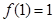 ,且
,且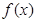 的导函数
的导函数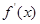 <
<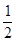 ,则
,则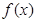 <
<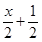 的解集为( )
的解集为( )
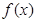 (
(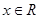 )满足
)满足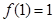 ,且
,且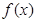 的导函数
的导函数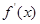 <
<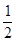 ,则
,则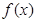 <
<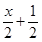 的解集为( )
的解集为( )A.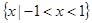 | B.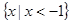 | C.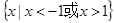 | D.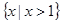 |
D
试题分析:设
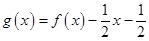
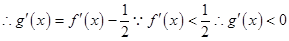
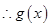 在R上是减函数
在R上是减函数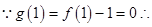 当
当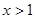 时
时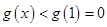 即
即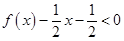
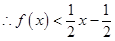 的解集为
的解集为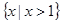
点评:求解抽象函数构成的不等式需要借助于函数单调性将抽象函数转化为具体函数,其间用到了不等式与函数间的转化,这种思路是不等式题目常用的转化方法

练习册系列答案
相关题目
题目内容
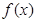 (
(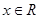 )满足
)满足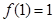 ,且
,且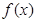 的导函数
的导函数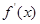 <
<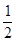 ,则
,则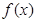 <
<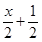 的解集为( )
的解集为( )A.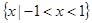 | B.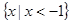 | C.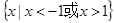 | D.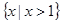 |
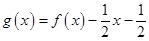
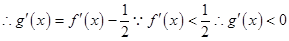
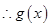 在R上是减函数
在R上是减函数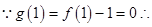 当
当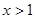 时
时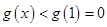 即
即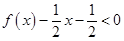
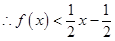 的解集为
的解集为