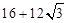题目内容
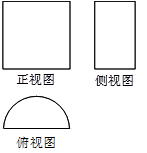
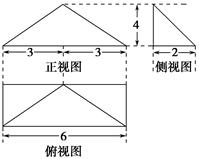
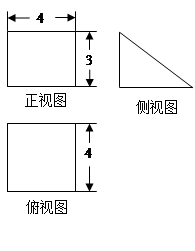
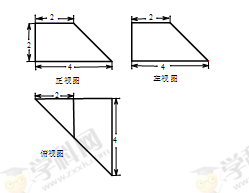
如图所示是一几何体的直观图、正(主)视图、侧(左)视图、俯视图.

(1)若F为PD的中点,求证:AF⊥面PCD;
(2)求几何体BEC-APD的体积.

(1)若F为PD的中点,求证:AF⊥面PCD;
(2)求几何体BEC-APD的体积.
(1)见解析(2)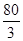
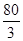
(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,PA∥EB,PA=2EB=4,PA=AD.∵PA=AD,F为PD的中点,∴PD⊥AF.
又∵CD⊥DA,CD⊥PA,DA∩PA=A,AD?平面PAD,PA?平面PAD,
∴CD⊥平面PAD,∴CD⊥AF.
又∵PD∩CD=D,∴AF⊥面PCD.
(2)VBEC-APD=VC-APEB+VP-ACD=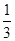 ×
×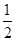 ×(4+2)×4×4+
×(4+2)×4×4+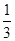 ×
×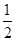 ×4×4×4=
×4×4×4=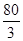 .
.
又∵CD⊥DA,CD⊥PA,DA∩PA=A,AD?平面PAD,PA?平面PAD,
∴CD⊥平面PAD,∴CD⊥AF.
又∵PD∩CD=D,∴AF⊥面PCD.
(2)VBEC-APD=VC-APEB+VP-ACD=
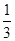 ×
×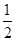 ×(4+2)×4×4+
×(4+2)×4×4+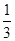 ×
×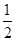 ×4×4×4=
×4×4×4=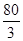 .
.
练习册系列答案
相关题目
 BB'=CC'=AB,则多面体ABC-A'B'C'的正视图是( )
BB'=CC'=AB,则多面体ABC-A'B'C'的正视图是( ) 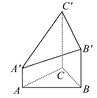

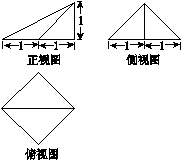
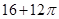

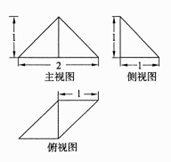
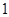 B.
B.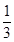 C.
C.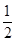 D.
D.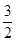


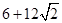 B.
B. 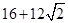 C.
C. D
D