题目内容
10.现有两组卡片,每组3张,牌面数字分别是1、2、3,从中各摸一张.(1)求摸出2张的牌面数字之和等于4的概率.
(2)摸出2张的牌面数字之和为多少时的概率最大?
分析 (1)用列举法求出基本事件数,计算对应的概率即可;
(2)根据(1)列举的基本事件数,分别计算摸出的牌面数字之和为t概率,求出概率最大对应的t值.
解答 解:(1)从两组卡片中各摸出一张,包含的基本事件数为
(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3)共9个,…(2分)
设摸出牌面数字之和为4的事件为A,A包含
(1,3);(2,2);(3,1)共3个基本事件,…(4分)
则$p(A)=\frac{3}{9}=\frac{1}{3}$;…(6分)
(2)从两组卡片中各摸出一张,牌面数字之和为t,
则t可以是2,3,4,5,6;…(8分)
由(1)知,P(t=2)=$\frac{1}{9}$,P(t=3)=$\frac{2}{9}$,
P(t=4)=$\frac{1}{3}$,P(t=5)=$\frac{2}{9}$,P(t=6)=$\frac{1}{9}$;…(10分)
所以,摸出牌面数字之和为4的概率最大.…(12分)
点评 本题考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
20.若0<x<y<1,则( )
| A. | 3y<3x | B. | x3>y3 | C. | log4x<log4y | D. | ($\frac{1}{4}$)x<($\frac{1}{4}$)y |
15.已知数列{an}、{bn}、{cn}的通项公式分别为:an=n,bn=n(n+1),cn=n(n+1)(n+2),数列{an},{bn}的前n项和分别为S1(n),S2(n),观察下表:
发现S1(n)=$\frac{1}{2}$bn,并可用下面方法证明:
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| an | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| S1(n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | … |
| bn | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | … |
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
2.下列说法错误的是( )
| A. | 设有一个回归方程为$\widehat{y}$=3-5x,则变量x每增加一个单位,y平均增加5个单位 | |
| B. | 回归直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点($\overline{x}$,$\overline{y}$) | |
| C. | 在一个2×2列联表中,由计算得随机变量K2的观测值k=13.079,则可以在犯错误的概率不超过0.001的前提下,认为这两个变量间有关系 | |
| D. | 将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变 |
15.为了研究某灌溉渠道水的流速y与水深x之间的关系,测得一组数据如下表:
(1)画出散点图,判断变量y与x是否具有相关关系;
(2)若y与x之间具有线性相关关系,求y对x的回归直线方程; ($\sum_{i=1}^5{x_i^2}=16.3$,$\sum_{i=1}^5{{x_i}{y_i}}=18.5$)
(3)预测水深为1.95m水的流速是多少.
参考公式:$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$.
| 水深x(m) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 流速y(m/s) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)若y与x之间具有线性相关关系,求y对x的回归直线方程; ($\sum_{i=1}^5{x_i^2}=16.3$,$\sum_{i=1}^5{{x_i}{y_i}}=18.5$)
(3)预测水深为1.95m水的流速是多少.
参考公式:$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$.
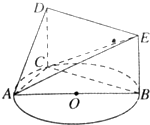 如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.
如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.