题目内容
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作互相垂直的两条直线分别与
作互相垂直的两条直线分别与![]() 相交于
相交于![]() ,
,![]() 和
和![]() ,
,![]() 四点.
四点.
(1)四边形![]() 能否成为平行四边形,请说明理由;
能否成为平行四边形,请说明理由;
(2)求![]() 的最小值.
的最小值.
【答案】(1)见解析.
(2)![]() .
.
【解析】
试题分析:(1)若四边形![]() 为平行四边形,则四边形
为平行四边形,则四边形![]() 为菱形, ∴
为菱形, ∴![]() 与
与![]() 在点
在点![]() 处互相平分,又
处互相平分,又![]() 的坐标为
的坐标为![]() 显然这时
显然这时![]() 不是平行四边形.
不是平行四边形.
(2)直线![]() 的斜率存在且不为零时,设直线
的斜率存在且不为零时,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,消去
,与椭圆方程联立,消去![]() ,利用韦达定理及弦长公式
,利用韦达定理及弦长公式![]() ,
,
令![]() ,则
,则![]() .考虑当直线
.考虑当直线![]() 的斜率不存在时和直线
的斜率不存在时和直线![]() 的斜率为零时情况得到
的斜率为零时情况得到![]() 的最小值
的最小值
试题解析:设点![]()
(Ⅰ)若四边形![]() 为平行四边形,则四边形
为平行四边形,则四边形![]() 为菱形,
为菱形,
∴![]() 与
与![]() 在点
在点![]() 处互相平分,又F的坐标为
处互相平分,又F的坐标为![]() ,由椭圆的对称性知
,由椭圆的对称性知![]() 垂直于
垂直于![]() 轴,则
轴,则![]() 垂直于
垂直于![]() 轴,
轴,
显然这时![]() 不是平行四边形.
不是平行四边形.
∴四边形![]() 不可能成为平行四边形.
不可能成为平行四边形.
(Ⅱ) 当直线![]() 的斜率存在且不为零时,设直线
的斜率存在且不为零时,设直线![]() 的方程为
的方程为![]()
由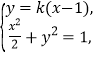 消去
消去![]() 得,
得,![]()
∴![]()
∴![]() 同理得,
同理得,![]() .∴
.∴![]() ,
,
令![]() ,则
,则![]() .
.
当直线![]() 的斜率不存在时,则
的斜率不存在时,则![]()
当直线![]() 的斜率为零时,则
的斜率为零时,则![]()
![]() ,∴
,∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
