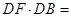题目内容
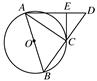
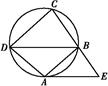
如图，AB是圆O的直径，点C在圆O上．延长BC到D使BC＝CD，过C作圆O的切线交AD于E.若AB＝6，ED＝2，则BC＝________.
2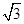
方法一：因为AB为圆O的直径，所以AC⊥BC.又BC＝CD，
所以△ABD是等腰三角形，所以AD＝AB＝6，∠DAC＝∠BAC.因为CE切圆O于点C，所以∠ECA＝∠ABC.又因为∠BAC＋∠ABC＝90°，所以∠DAC＋∠ECA＝90°，故CE⊥AD.故CD2＝DE·DA＝2×6＝12，
所以BC＝CD＝2.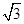
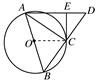
方法二：如图，连接OC，因为BO＝OA，BC＝CD，所以OC∥AD.又因为CE切圆O于点C，所以OC⊥CE，所以AD⊥CE.因为AB为圆O的直径，所以AC⊥BD.又BC＝CD，所以△ABD是等腰三角形，故∠ADB＝∠ABD，所以△ABC∽△CDE，则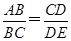
，所以BC·CD＝AB·DE，即BC2＝AB·DE＝6×2＝12，BC＝2.
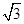所以△ABD是等腰三角形，所以AD＝AB＝6，∠DAC＝∠BAC.因为CE切圆O于点C，所以∠ECA＝∠ABC.又因为∠BAC＋∠ABC＝90°，所以∠DAC＋∠ECA＝90°，故CE⊥AD.故CD2＝DE·DA＝2×6＝12，
所以BC＝CD＝2
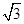.方法二：如图，连接OC，因为BO＝OA，BC＝CD，所以OC∥AD.又因为CE切圆O于点C，所以OC⊥CE，所以AD⊥CE.因为AB为圆O的直径，所以AC⊥BD.又BC＝CD，所以△ABD是等腰三角形，故∠ADB＝∠ABD，所以△ABC∽△CDE，则
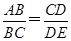，所以BC·CD＝AB·DE，即BC2＝AB·DE＝6×2＝12，BC＝2.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
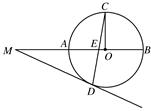
，求MA及CE的长．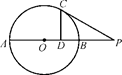
的弦ED，CB的延长线交于点A，若BD
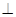AE，AB＝4,BC＝2,AD＝3,则CE＝ ; 
的⊙O中，弦AB，CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．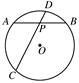
，垂足为F，若
，
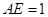，则
