题目内容
已知a,b,c均为正数,证明:a2+b2+c2+ 2≥6
2≥6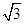 ,并确定a,b,c为何值时,等号成立.
,并确定a,b,c为何值时,等号成立.
 2≥6
2≥6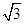 ,并确定a,b,c为何值时,等号成立.
,并确定a,b,c为何值时,等号成立.见解析
法一:因为a、b、c均为正数,由平均值不等式得
a2+b2+c2≥3(abc) ,①
,①
 ≥3(abc)-
≥3(abc)- ,②
,②
所以 2≥9(abc)-
2≥9(abc)- .
.
故a2+b2+c2+ 2≥3(abc)
2≥3(abc) +9(abc)-
+9(abc)- .
.
又3(abc) +9(abc)-
+9(abc)- ≥2
≥2 =6
=6 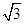 ,③
,③
所以原不等式成立.
当且仅当a=b=c时,①式和②式等号成立.
当且仅当3(abc) =9(abc)-
=9(abc)- 时,③式等号成立.
时,③式等号成立.
即当且仅当a=b=c=3 时,原式等号成立.
时,原式等号成立.
法二:因为a,b,c均为正数,由基本不等式得
a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac,
所以a2+b2+c2≥ab+bc+ac.①
同理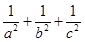 ≥
≥ ,②
,②
故a2+b2+c2+ 2≥ab+bc+ac+3
2≥ab+bc+ac+3 +3
+3 +3
+3 ≥6
≥6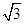 .③
.③
所以原不等式成立,
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c=3 时,原式等号成立.
时,原式等号成立.
a2+b2+c2≥3(abc)
 ,①
,① ≥3(abc)-
≥3(abc)- ,②
,②所以
 2≥9(abc)-
2≥9(abc)- .
.故a2+b2+c2+
 2≥3(abc)
2≥3(abc) +9(abc)-
+9(abc)- .
.又3(abc)
 +9(abc)-
+9(abc)- ≥2
≥2 =6
=6 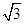 ,③
,③所以原不等式成立.
当且仅当a=b=c时,①式和②式等号成立.
当且仅当3(abc)
 =9(abc)-
=9(abc)- 时,③式等号成立.
时,③式等号成立.即当且仅当a=b=c=3
 时,原式等号成立.
时,原式等号成立.法二:因为a,b,c均为正数,由基本不等式得
a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac,
所以a2+b2+c2≥ab+bc+ac.①
同理
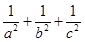 ≥
≥ ,②
,②故a2+b2+c2+
 2≥ab+bc+ac+3
2≥ab+bc+ac+3 +3
+3 +3
+3 ≥6
≥6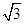 .③
.③所以原不等式成立,
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c=3
 时,原式等号成立.
时,原式等号成立.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
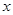 是
是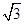 的一个近似值,令
的一个近似值,令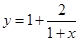 .
.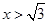 ,求证:
,求证: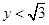 ;
;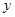 与
与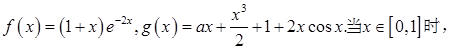

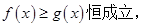
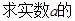 取值范围.
取值范围. , 求证:
, 求证: .
.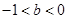 ,
, ,那么下列不等式成立的是( )
,那么下列不等式成立的是( )



 ,1+
,1+ >1,1+
>1,1+ +
+ + +
+ + >
> ,1+
,1+ >2,1+
>2,1+ >
> , ,由此猜测第n个不等式为 (n∈N*).
, ,由此猜测第n个不等式为 (n∈N*). 且
且 ,
, 为大于1的自然数,
为大于1的自然数,