题目内容
11.函数f(x)的定义域为(0,1],则函数f(lg$\frac{{x}^{2}+x}{2}$)的定义域为( )| A. | [-1,4] | B. | [-5,-2] | C. | [-5,-2]∪[1,4] | D. | [-5,-2)∪(1,4] |
分析 根据条件和对数函数的性质列出不等式组,利用对数函数的单调性求解可得到函数的定义域.
解答 解:由题意得,$\left\{\begin{array}{l}{\frac{{x}^{2}+x}{2}>0}\\{0<lg\frac{{x}^{2}+x}{2}≤1}\end{array}\right.$,即$1<\frac{{x}^{2}+x}{2}≤10$,
解得-5≤x<-2或1<x≤4,
所以函数的定义域是[-5,-2)∪(1,4],
故选:D.
点评 本题考查函数的定义域,以及对数函数的性质的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列给出的输入语句、输出语句和赋值语句:则其中正确的个数是( )
(1)输出语句INPUT a,b,c
(2)输入语句INPUT x=3
(3)赋值语句3=A
(4)赋值语句A=B=C.
(1)输出语句INPUT a,b,c
(2)输入语句INPUT x=3
(3)赋值语句3=A
(4)赋值语句A=B=C.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.已知集合A={-2,-1,0,1,2,3},集合$B=\{x∈R|-1≤x<\frac{3}{2}\}$,则A∩B等于( )
| A. | {-2,-1,0,1} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {-1,0,1,2,3} |
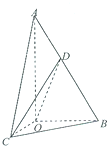 如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C的直二面角,D是AB的中点.
如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C的直二面角,D是AB的中点.