题目内容
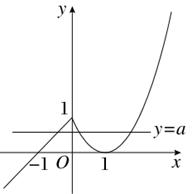
已知函数f(x)= 若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
 若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )| A.(0,1) | B.(0,2) | C.(1,2) | D.(0,3) |
A
设t=f(x),则方程为t2-at=0,解得t=0或t=a,即f(x)=0或f(x)=a.如图,作出函数f(x)的图象,由函数图象,可知f(x)=0的解有两个,故要使方程f2(x)-af(x)=0恰有5个不同的解,则方程f(x)=a的解必有三个,此时0<a<1.所以a的取值范围是(0,1).


练习册系列答案
相关题目
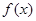 是二次函数,不等式
是二次函数,不等式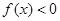 的解集是(0,5),且
的解集是(0,5),且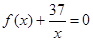 在区间
在区间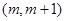 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.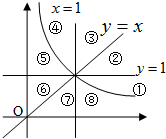
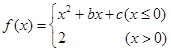 ,若
,若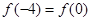 ,
,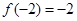 ,则关于
,则关于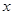 的方程
的方程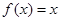 的解的个数为 ( )
的解的个数为 ( ) ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 是函数
是函数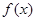 的导函数,求函数
的导函数,求函数 上的最小值;
上的最小值; ,函数
,函数 内有零点,求
内有零点,求 的取值范围
的取值范围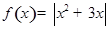 ,
,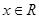 .若方程
.若方程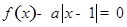 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数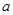 的取值范围为__________.
的取值范围为__________. -
- (a>0)没有零点,则实数a的取值范围为________.
(a>0)没有零点,则实数a的取值范围为________. )x-sinx在区间[0,2π]上的零点个数为( )
)x-sinx在区间[0,2π]上的零点个数为( )