题目内容
已知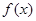 是二次函数,不等式
是二次函数,不等式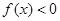 的解集是(0,5),且
的解集是(0,5),且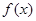 在区间[-1,4]上的最大值是12.
在区间[-1,4]上的最大值是12.
(1)求f(x)的解析式;
(2)是否存在正整数m,使得方程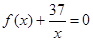 在区间
在区间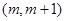 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
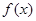 是二次函数,不等式
是二次函数,不等式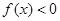 的解集是(0,5),且
的解集是(0,5),且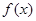 在区间[-1,4]上的最大值是12.
在区间[-1,4]上的最大值是12.(1)求f(x)的解析式;
(2)是否存在正整数m,使得方程
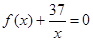 在区间
在区间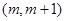 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.(1)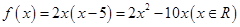 ;(2)方程
;(2)方程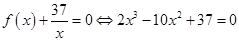 ,
,
设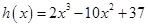 ,则
,则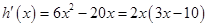 .
.
当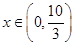 时,
时,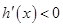 ,
,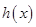 是减函数;当
是减函数;当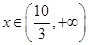 时,
时,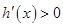 ,
,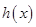 是增函数.
是增函数.
因为 .所以方程
.所以方程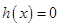 在区间
在区间 ,
, 内分别有唯一实数根,而区间
内分别有唯一实数根,而区间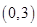 ,
,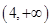 内没有实数根.所以存在唯一的正数
内没有实数根.所以存在唯一的正数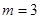 ,使得方程
,使得方程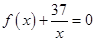 在区间
在区间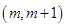 内有且只有两个不等的实数根.
内有且只有两个不等的实数根.
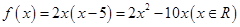 ;(2)方程
;(2)方程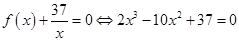 ,
,设
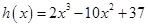 ,则
,则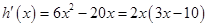 .
.当
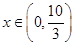 时,
时,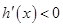 ,
,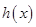 是减函数;当
是减函数;当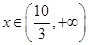 时,
时,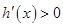 ,
,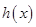 是增函数.
是增函数.因为
 .所以方程
.所以方程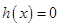 在区间
在区间 ,
, 内分别有唯一实数根,而区间
内分别有唯一实数根,而区间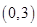 ,
,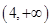 内没有实数根.所以存在唯一的正数
内没有实数根.所以存在唯一的正数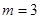 ,使得方程
,使得方程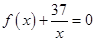 在区间
在区间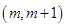 内有且只有两个不等的实数根.
内有且只有两个不等的实数根.试题分析:(1)由已知得0,5是二次函数
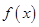 的两个零点值,所以可设
的两个零点值,所以可设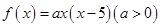 ,开口方向向上,对称轴为
,开口方向向上,对称轴为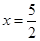 ,因此
,因此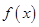 在区间
在区间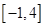 上的最大值是
上的最大值是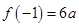 ,则
,则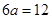 ,即
,即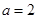 ,因此可求出函数
,因此可求出函数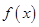 的解析式;(2)由(1)得
的解析式;(2)由(1)得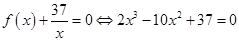 ,构造函数
,构造函数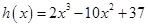 ,则方程
,则方程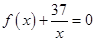 的实数根转化为函数
的实数根转化为函数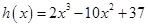 的零点,利用导数法得到函数
的零点,利用导数法得到函数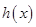 减区间为
减区间为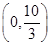 、增区间为
、增区间为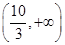 ,又有
,又有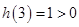 ,
,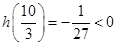 ,
,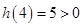 ,发现函数
,发现函数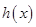 在区间
在区间 ,
, 内分别有唯一零点,而在区间
内分别有唯一零点,而在区间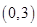 ,
,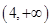 内没有零点,所以存在唯一的正数
内没有零点,所以存在唯一的正数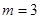 ,使得方程
,使得方程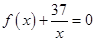 在区间
在区间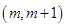 内有且只有两个不等的实数根.
内有且只有两个不等的实数根.(1)因为
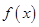 是二次函数,且
是二次函数,且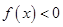 的解集是
的解集是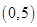 ,
,所以可设
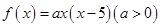 2分
2分所以
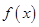 在区间
在区间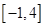 上的最大值是
上的最大值是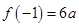 . 4分
. 4分由已知,得
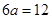 ,
,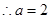 .
.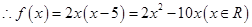 . 6分
. 6分(2)方程
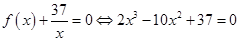 ,
,设
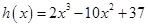 ,则
,则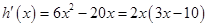 . 10分
. 10分当
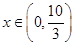 时,
时,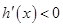 ,
,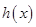 是减函数;
是减函数;当
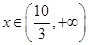 时,
时,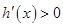 ,
,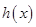 是增函数. 10分
是增函数. 10分因为
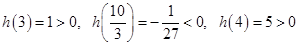 .
.所以方程
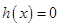 在区间
在区间 ,
, 内分别有唯一实数根,而区间
内分别有唯一实数根,而区间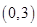 ,
,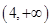 内没有实数根. 12分
内没有实数根. 12分所以存在唯一的正数
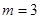 ,使得方程
,使得方程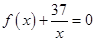 在区间
在区间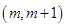 内有且只有两个不等的实数根. 14分
内有且只有两个不等的实数根. 14分
练习册系列答案
相关题目
 若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )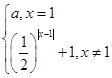 ,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.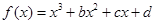 的大致图象,则
的大致图象,则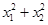 等于
等于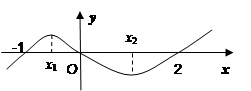
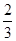
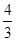
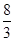
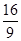
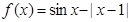 的零点个数为 .
的零点个数为 .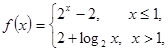 则函数
则函数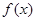 的零点为( )
的零点为( )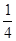 和1
和1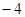 和0
和0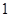
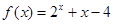 ,则函数
,则函数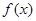 的零点位于区间( )
的零点位于区间( )