题目内容

14．设{an}为递增的正整数数列，an+2=an+an+1（n∈N*）若a5=24，则a6=39．

分析 根据an+2=an+an+1分析出a5与a1、a2的关系，再根据an是正整数和a5=24，求出a1、a2的值，即可求出a6的值．

解答 解：由an+2=an+an+1，n∈N*，且an是正整数，
因为数列{an}为递增数列，所以an+2＞an+1，n∈N*，
设a1的值是X，a2的值是Y，则Y＞X，
由an+2=an+an+1得：a3=X+Y，a4=X+2Y，a5=2X+3Y=24＞5X，
所以X＜4，又X、Y必须为整数，则X=3、Y=6，
所以a6=3X+5Y=39，
故答案为：39．

点评 本题以数列为背景考查逻辑推理知识，考查分析问题、解决问题的能力，属于中档题．

练习册系列答案
相关题目
4．已知命题p：对任意实数x都有x2+ax+a＞0恒成立；
命题q：关于x的方程x2-x+a=0有实数根；
如果“p或q”为真命题，“p且q”为假命题，求实数a的取值范围．
5．已知二次函数f（x）=ax2+bx+c，若f（1）=1，f（2）=2，则f（2+k）-f（1-k）=2k+1．
2．已知函数f（x）=-x2+（a-1）x+a-1，g（x）=x（x-a）2-1，其中a为实数．
（1）是否存在x0∈（0，1），使得f（x0）+1=0？若存在，求出实数a的取值范围；若不存在，请说明理由．
（2）若集合A={x|f（x）•g（x）=0，x∈R}中恰有5个元素，求实数a的取值范围．
9．复数ω=$\frac{3i-1}{i}$的虚部和模依次是（　　）
A．3，2$\sqrt{2}$B．3i，$\sqrt{10}$C．1，$\sqrt{10}$D．-1，2$\sqrt{2}$
19．求值：
（1）$\frac{sin29°-sin31°}{cos29°-cos31°}$；
（2）$\frac{3-sin70°}{2-co{s}^{2}10°}$；
（3）$\frac{sin7°+sin8°cos15°}{cos7°-sin8°sin165°}$．
6．已知在△ABC中，a，b，c分别为内角A，B，C的对边，且满足cos2A+2sin2B+2sin2C-2$\sqrt{3}$sinBsinC=1．
（1）求角A的大小；
（2）若b=$\sqrt{3}$，c=4，求△ABC的外接圆的面积．
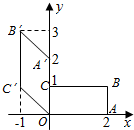3．如图，矩形OABC在变换T的作用下变成了平行四边形OA′B′C′，变换T所对应的矩阵为M，矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍，纵坐标伸长到原来的3倍的变换所对应的矩阵．
（Ⅰ）求矩阵M，N；
（Ⅱ）直线l先在矩阵M，再在矩阵N所对应的线性变换作用下像的方程为x+y+1=0．求直线l的方程．
4．关于下列命题
①函数y=4sin（2x-$\frac{π}{3}$）的一个对称中心是（$\frac{π}{6}$，0）；
②函数y=sin（x+$\frac{π}{4}$）在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上是增函数；
③函数y=cos2（$\frac{π}{4}$-x）是偶函数；
④函数y=tanx在第一象限是增函数；
其中正确命题序号为①．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网