题目内容

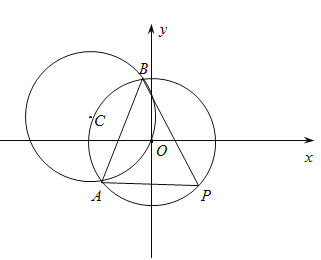
【题目】已知点,是函数图象上的任意两点,且角的终边经过点,若时,的最小值为．

（1）求函数的解析式；

（2）若方程在内有两个不同的解,求实数的取值范围．

【答案】(1)；(2) 或..

【解析】

(1)由角的终边经过点可得，由时,的最小值为可得周期，即得，即可求出函数的解析式；（2）先解得在的值域，将问题转化成一元二次方程在给定的范围内解的个数问题，再将一元二次方程个数问题转化成二次函数与直线交点为个数问题，可解得的值.

（1）角的终边经过点，，，．

由时,的最小值为，得，即，．

∴

(2）∴，∴．设，

问题转化研究方程在（0，2）内解的情况．

当时方程在（0，2）内解只有一个，对应x的解有两个

∴m的取值范围是：或.

【点晴】

本题考查三角函数的定义、三角函数解析式以及根据函数零点求参数，考查了转化与化归的思想，以及数形结合解决问题的能力．本题属于难题.

练习册系列答案
相关题目

【题目】在平面直角坐标系中，已知圆与圆关于直线对称.

（1）求直线的方程；

（2）设圆与圆交于点、，点为圆上的动点，求面积的最大值.

【题目】已知数列的前项和为，且满足:

(1)证明：是等比数列，并求数列的通项公式.

(2)设，若数列是等差数列，求实数的值；

(3)在(2)的条件下，设 记数列的前项和为，若对任意的存在实数,使得,求实数的最大值.

【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰:“我羊食半马、“马主曰:“我马食半牛，”今欲衰偿之，问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半，”马主人说:“我马所吃的禾苗只有牛的一半，“打算按此比例偿还，他们各应偿还多少？该问题中，1斗为10升，则马主人应偿还( )升粟？

A. B. C. D.

【题目】下列说法错误的是（ ）

A.命题“若，则”的逆否命题为：“若，则”

B.“”是“”的充分而不必要条件

C.若且为假命题，则、均为假命题

D.命题“存在，使得”，则非“任意，均有”

【题目】如图，在四棱锥中，为矩形，是以为直角的等腰直角三角形，平面平面．

（Ⅰ）证明：平面平面；

（Ⅱ）为直线的中点，且，求二面角的正弦值．

【题目】某企业通过调查问卷（满分50分）的形式对本企业900名员工的工作满意程度进行调查，并随机抽取了其中30名员工（16名女工，14名男工）的得分，如下表：

女

47

36

32

48

34

44

43

47

46

41

43

42

50

43

35

49

男

37

35

34

43

46

36

38

40

39

32

48

33

40

34

（1）根据以上数据，估计该企业得分大于45分的员工人数；

（2）现用计算器求得这30名员工的平均得分为40.5分，若规定大于平局得分为 “满意”，否则为 “不满意”，请完成下列表格：

“满意”的人数

“不满意”的人数

合计

女员工

16

男员工

14

合计

30

（3）根据上述表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下，认为该企业员工“性别”与“工作是否满意”有关？

参考数据：

P(K2K)

0.10

0.050

0.025

0.010

0.001

K

2.706

3.841

5.024

6.635

10.828

【题目】一个盒子里装有大小均匀的6个小球，其中有红色球4个，编号分别为1，2，3，4；白色球2个，编号分别为4，5，从盒子中任取3个小球（假设取到任何—个小球的可能性相同）.

（1）求取出的3个小球中，含有编号为4的小球的概率；

（2）在取出的3个小球中，小球编号的最大值设为，求随机变量的分布列及数学期望.

【题目】已知函数.

（Ⅰ）求函数的单调区间;

（Ⅱ）当时，证明：对任意的.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网