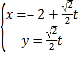题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 与圆
与圆![]() 关于直线对称.
关于直线对称.
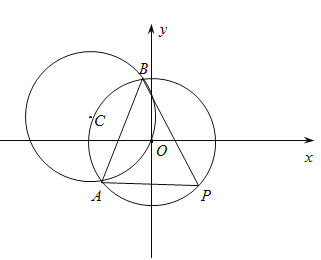
(1)求直线的方程;
(2)设圆![]() 与圆
与圆![]() 交于点
交于点![]() 、
、![]() ,点
,点![]() 为圆
为圆![]() 上的动点,求
上的动点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 根据题意知,所求的直线与直线
根据题意知,所求的直线与直线![]() 垂直,且经过
垂直,且经过![]() 的中点,分别求出点
的中点,分别求出点![]() 和点
和点![]() 的坐标,然后代入点斜式求解即可.
的坐标,然后代入点斜式求解即可.
![]() 由(1)得:直线
由(1)得:直线![]() 的方程为
的方程为![]() ,由圆
,由圆![]() 和圆
和圆![]() 关于直线对称可知,圆
关于直线对称可知,圆![]() 的半径与圆
的半径与圆![]() 的半径相等为
的半径相等为![]() ,利用弦长公式求出弦长
,利用弦长公式求出弦长![]() ,要使
,要使![]() 的面积最大,只需点
的面积最大,只需点![]() 到直线
到直线![]() 的距离最大,结合图形可知,当
的距离最大,结合图形可知,当![]() 时,
时,![]() 的面积最大,求出此时
的面积最大,求出此时![]() 的面积即可.
的面积即可.
(1)把圆![]() 的方程化为
的方程化为![]() ,
,
所以圆心![]() ,半径为
,半径为![]() ,因为
,因为![]() ,
,
所以![]() 的中点为
的中点为![]() ,
,![]() .
.
由已知条件得,所求直线与直线![]() 垂直,且经过
垂直,且经过![]() 的中点
的中点![]() ,
,
即直线经过点![]() ,且斜率
,且斜率![]() ,
,
所以所求直线方程为![]() ,
,
即![]() 即为所求的直线方程.
即为所求的直线方程.
(2)由(1)得:直线![]() 的方程为
的方程为![]() ,
,
由点到直线的距离公式可得,
圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
因为圆![]() 和圆
和圆![]() 关于直线对称,
关于直线对称,
所以圆![]() 的半径与圆
的半径与圆![]() 的半径相等为
的半径相等为![]() ,
,
所以弦长![]() ,
,
要使![]() 的面积最大,只需点
的面积最大,只需点![]() 到直线
到直线![]() 的距离最大,
的距离最大,
结合图形可知,当![]() 时,
时,![]() 的面积最大,
的面积最大,
此时点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
此时![]() 的面积为
的面积为![]()
![]() .
.
所以![]() 面积的最大值为
面积的最大值为![]() .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】纪念币是一个国家为纪念国际或本国的政治、历史,文化等方面的重大事件、杰出人物、名胜古迹、珍稀动植物、体育赛事等而发行的法定货币.我国在 1984 年首次发行纪念币,目前已发行了 115 套纪念币,这些纪念币深受邮币爱好者的喜爱与收,2019 年发行的第 115 套纪念币“双遗产之泰山币”是目前为止发行的第一套异形币,因为这套纪念币的多种特质,更加受到爱好者追捧.某机构为调查我国公民对纪念币的喜爱态度,随机选了某城市某小区的 50 位居民调查,调查结果统计如下:
喜爱 | 不喜爱 | 合计 | |
年龄不大于40岁 | 24 | ||
年龄大于40岁 | 40 | ||
合计 | 22 | 50 |
(1)根据已有数据,把表格数据填写完整;
(2)判断能否在犯错误的概率不超过 1% 的前提下认为不同年龄与纪念币的喜爱无关?